最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个 $n \times m$ 的矩阵，$A$ 在矩阵左上角 $(1,1)$ 的位置，$B$ 在矩阵右下角 $(n,m)$ 的位置

$A$ 要向 $B$ 传递一次纸条，且传递的过程只能向下或向右

$B$ 也要向 $A$ 传递一次纸条，且传递的过程只能向上或向左

两次过程中，经过的格子不能重合

每个格子给定一个好感度，其实就是这个格子的价值

我们要找到一个方案，使得两次传递的路线经过的所有格子的价值最大

题目解析

这题明显不是一个裸题，我们需要一层一层的拆解分析

首先想到的是能不能往 方格取数 模型上靠

对于一个从 $(n,m)$ 出发到 $(1,1)$ 的路线，且只能向上或向右走，考虑将其方向调转，则必定对应一条从 $(1,1)$ 出发到 $(n,m)$ 的路线，且只能向下或向右走

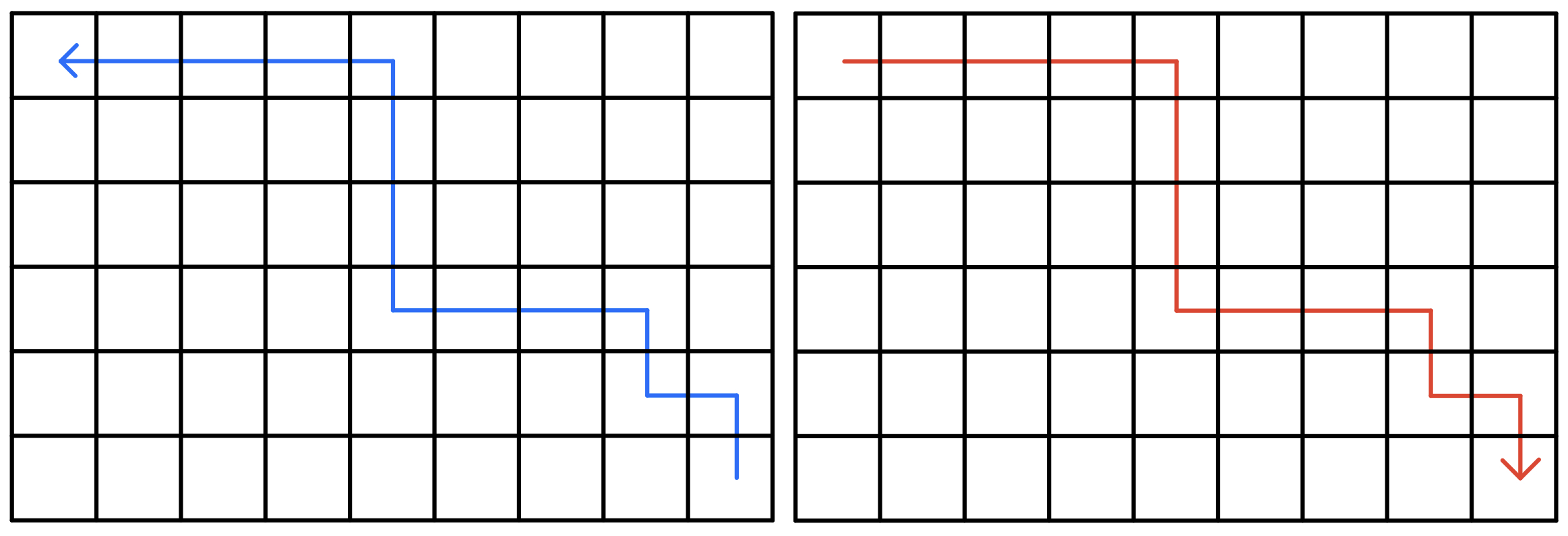
这两种走法的方案都是一一对应的（即任意一条路线都可以找到其对应的反向路线），因此该方案映射合法

于是该问题就变成了寻找一条从 $(1,1)$ 出发到达 $(n,m)$，每次只能向下或向右走，先后出发两次，且两次路线不能经过重复格子的最大价值方案

这样就很靠近 方格取数 模型了

关于如何解决不能经过重复格子的问题

我们先给定一个结论： 方格取数 dp模型的最优方案可以是不经过重复格子的

证明：

情况一：最优解的两条路线是相互交叉经过的

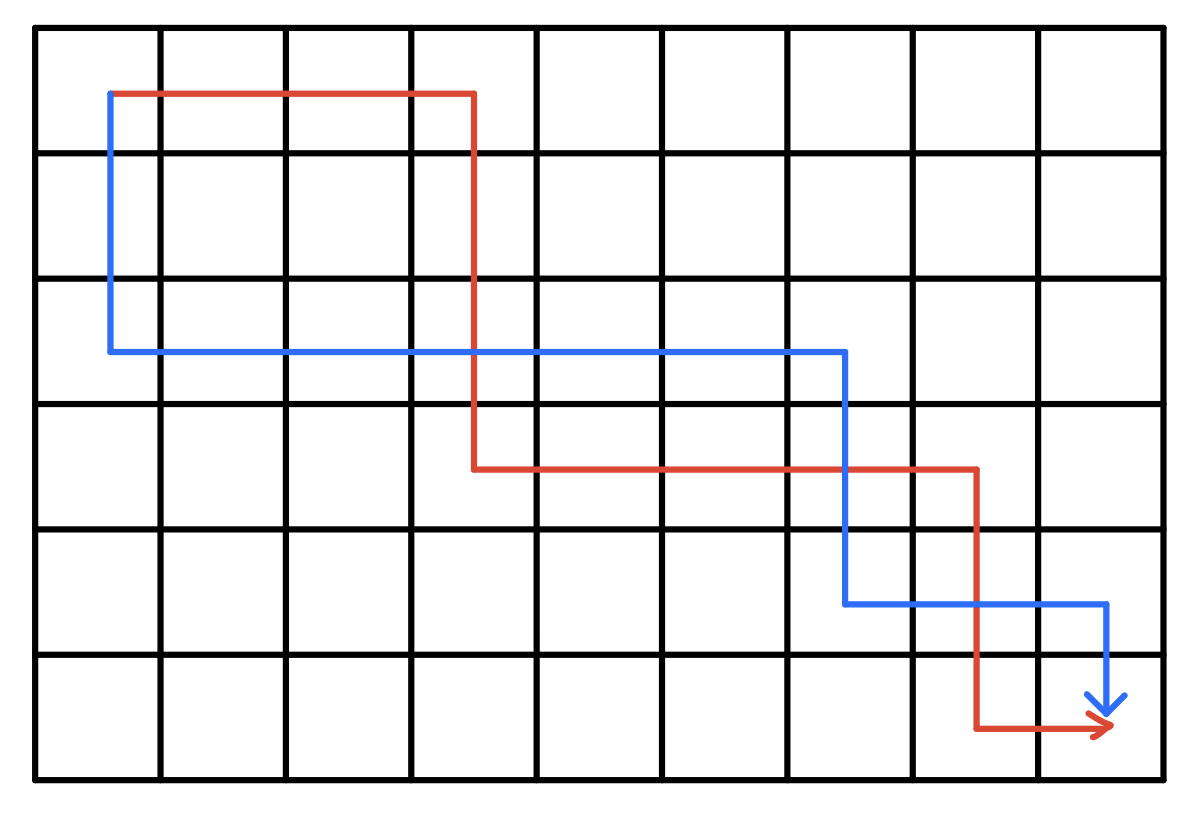
则我们可以对交叉出来的部分进行路线交换，如下图的操作

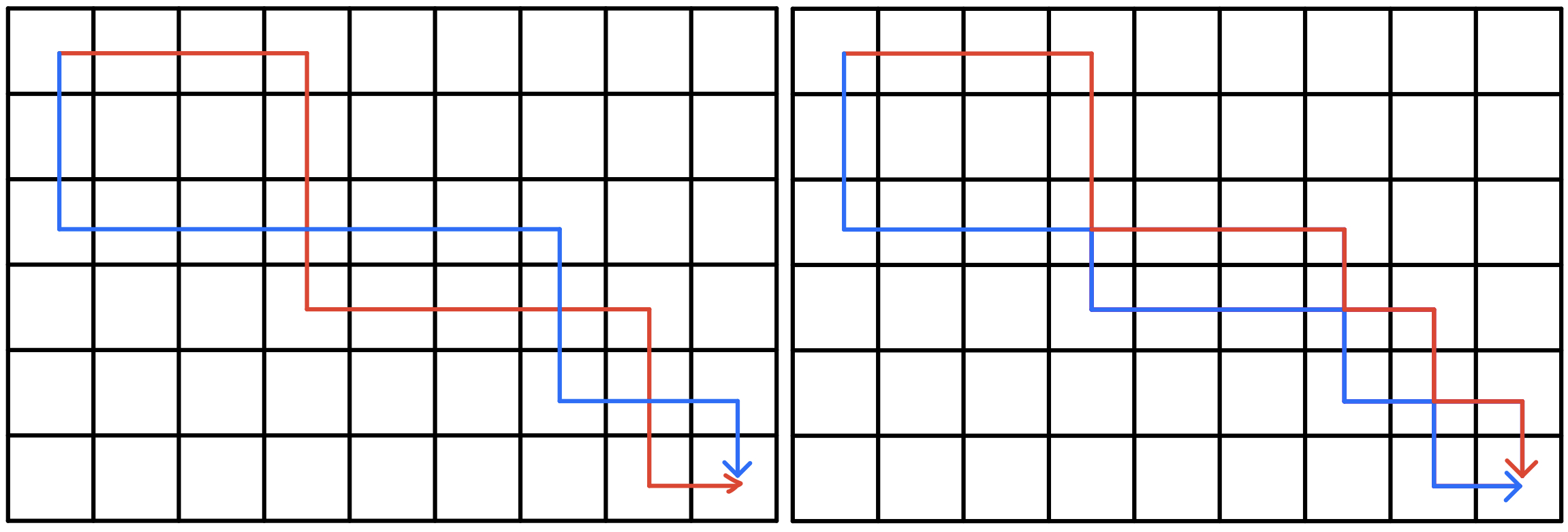
于是，我们可以发现，所有的交叉路线都会映射成一种一条路线只在下方走，一条路线只在上方走的不交叉路线

因此我们只需集中解决情况二即可

情况二：最优解的两条路线不交叉，但在某些点有重合

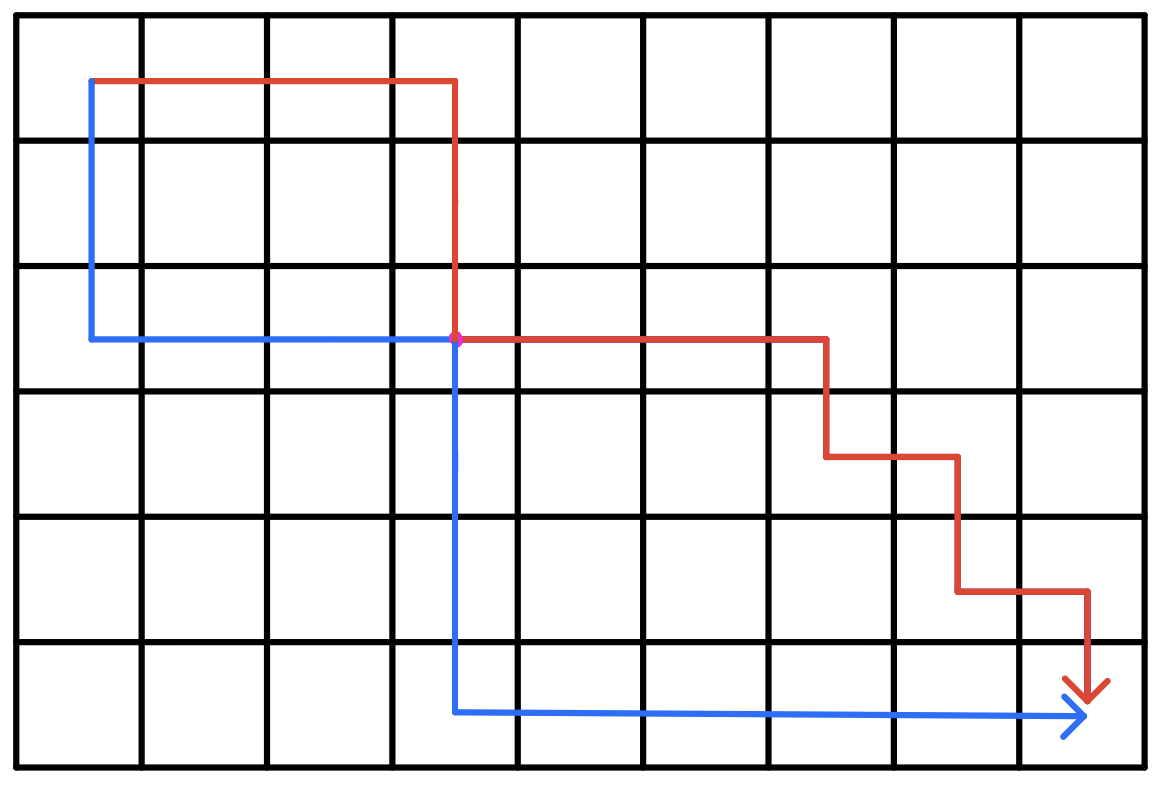
由于方格取数，对于走到相同格子时，只会累加一次格子的价值

于是我们可以使用贪心中的微调法来进行这部分的证明

对于重合的格子，我们必然可以在两条路线中找到额外的一条或两条路线，使得新的路线不发生重合

具体参照下图：

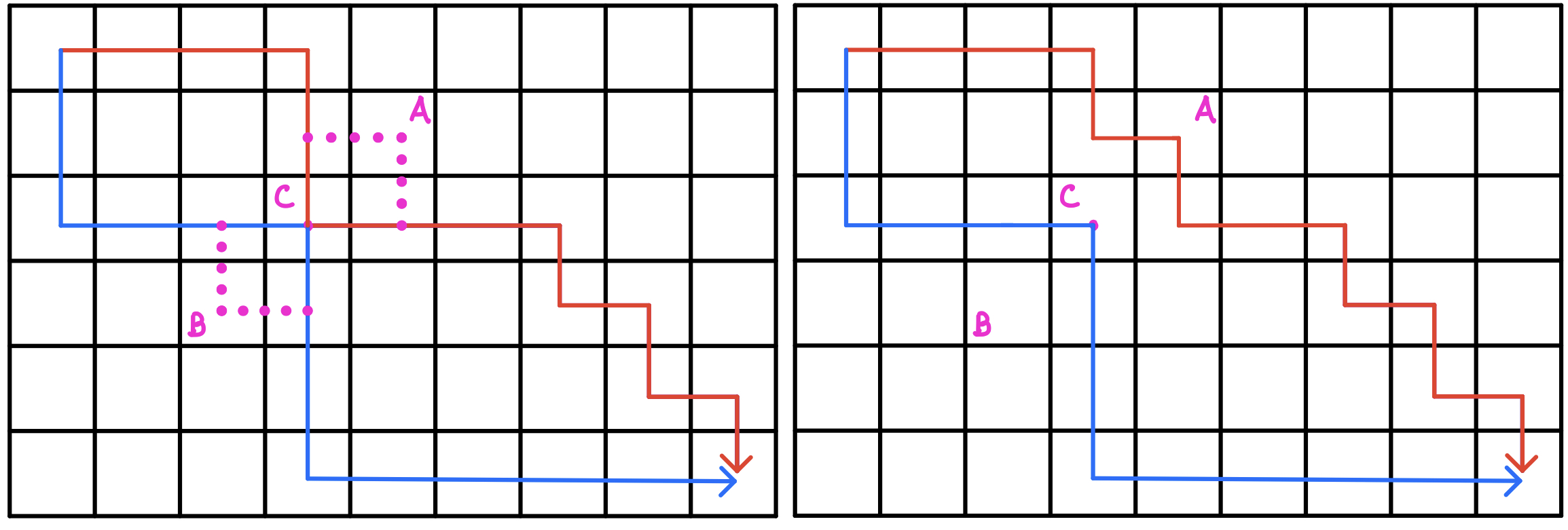
由于原路线是最优解，则必然 $w_A = w_B = 0$，否则最优解路线必然是经过 $A$ 或 $B$ 的

因此，我们可以通过微调其中的一条路线，使之不经过重合点 $C$，同时路线的总价值没有减少

得证：最优解路线可以是不经过重复路线的 （部分证明方法参照了第一赞的题解了）

接下来就是完全参照 AcWing 1027. 方格取数 的DP分析了

关于重合格子判断一些条件都在这篇博客里详细写了

这里我偷个懒，直接用我上篇博客的内容了 （既然是我自己写的应该不算抄袭吧！）

闫氏DP分析法

$$ \begin{cases} 状态表示f_{k,i,j} \begin{cases} 属性: 路径长度为k,第一条路线到x_1=i,第二条路线到x_2=j的所有方案 \\\ 集合: 方案中的路线经过的所有物品的总价值最大 Max \end{cases} \\\ 状态转移 f_{k,i,j} = max\{f_{k-1,i,j},f_{k-1,i-1,j},f_{k-1,i,j-1},f_{k-1,i-1,j-1}\} + w \end{cases} $$

集合划分

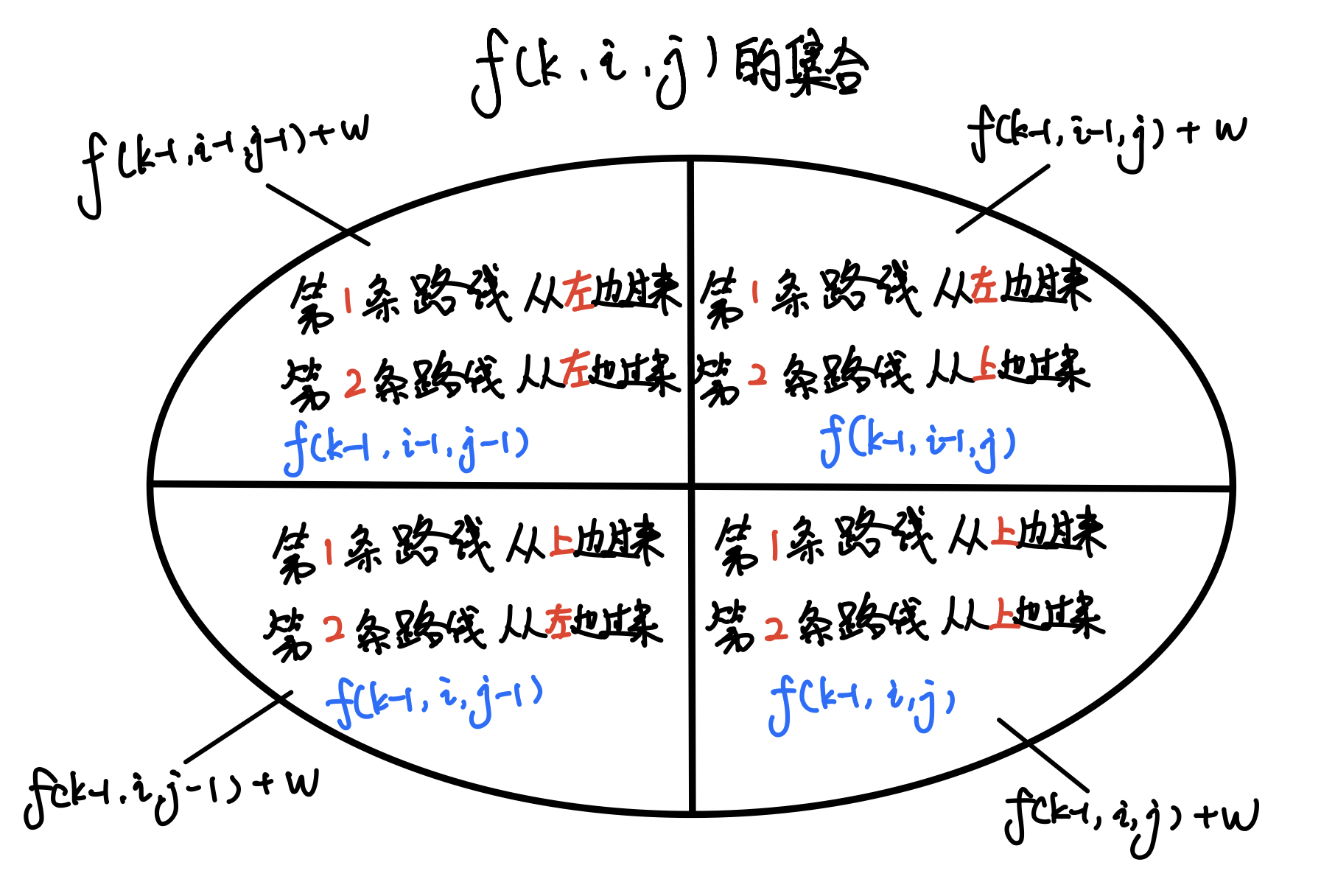
状态的初值: f[2][1][1]

目标的状态: f[n + m][n][m]

Code(三重迭代写法)

#include <iostream>

using namespace std;

const int N = 55, M = 2 * N;

int n, m;
int w[N][N];
int f[M][N][N];

int main()
{
    //input
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 1; j <= m; ++ j)
        {
            cin >> w[i][j];
        }
    }
    //dp
    for (int k = 2; k <= n + m; ++ k)
    {
        for (int i = 1; i < k && i <= n; ++ i)
        {
            for (int j = 1; j < k && j <= n; ++ j)
            {
                int v = w[i][k - i];
                if (i != j) v += w[j][k - j];

                int &t = f[k][i][j];
                t = max(t, f[k - 1][i][j]);
                t = max(t, f[k - 1][i - 1][j]);
                t = max(t, f[k - 1][i][j - 1]);
                t = max(t, f[k - 1][i - 1][j - 1]);
                t += v;
            }
        }
    }

    //output
    cout << f[n + m][n][n] << endl;
    return 0;
}

Code(记忆化搜索写法)

#include <iostream>
#include <cstring>

using namespace std;

const int N = 55, M = 2 * N, INF = 0x3f3f3f3f;

int n, m;
int w[N][N];
int f[M][N][N];

int dp(int k, int i, int j)
{
    if (f[k][i][j] >= 0) return f[k][i][j];

    if (k == 2 && i == 1 && j == 1) return f[k][i][j] = w[1][1];

    if (i <= 0 || i >= k || j <= 0 || j >= k) return -INF;

    int v = w[i][k - i];
    if (i != j) v += w[j][k - j];

    int t = 0;
    t = max(t, dp(k - 1, i, j));
    t = max(t, dp(k - 1, i - 1, j));
    t = max(t, dp(k - 1, i, j - 1));
    t = max(t, dp(k - 1, i - 1, j - 1));
    return f[k][i][j] = t + v;
}
int main()
{
    //input
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 1; j <= m; ++ j)
        {
            cin >> w[i][j];
        }
    }
    //initialize
    memset(f, -1, sizeof f);
    //output
    cout << dp(n + m, n, n) << endl;
    return 0;
}