$\color{green}{<–画图不易，点下这里赞一下吧}$
视频讲解： https://www.acwing.com/video/5399/
如何用 dfs 解决全排列问题？
dfs 最重要的是搜索顺序。用什么顺序遍历所有方案。
对于全排列问题，以 n = 3 为例，可以这样进行搜索：
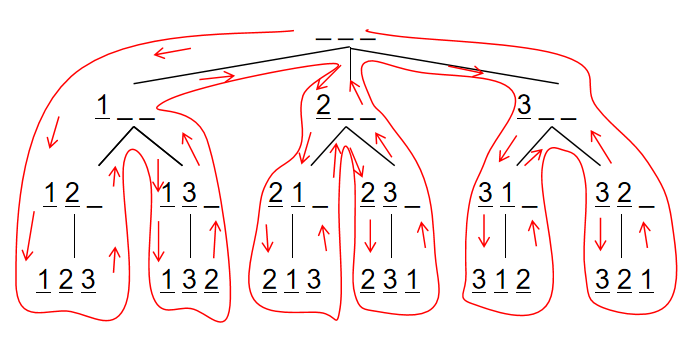
假设有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。
最开始的时候，三个空位都是空的： __
首先填写第一个空位，第一个空位可以填 1，填写后为：1
填好第一个空位，填第二个空位，第二个空位可以填 2，填写后为：1 2 __
填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为： 1 2 3
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填。
因此再往后退一步，退到了状态：1 。第二个空位上除了填过的 2，还可以填 3。第二个空位上填写 3，填写后为：1 3 __
填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为： 1 3 2
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。
因此再往后退一步，退到了状态：1 。第二个空位上除了填过的 2，3，没有其他数字可以填。
因此再往后退一步，退到了状态： 。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 __
填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：2 1 __
填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为：2 1 3
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3，没有其他数字可以填。
因此再往后退一步，退到了状态：2 。第二个空位上除了填过的 1，还可以填 3。第二个空位上填写 3，填写后为：2 3 __
填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：2 3 1
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，没有其他数字可以填。
因此再往后退一步，退到了状态：2 。第二个空位上除了填过的 1，3，没有其他数字可以填。
因此再往后退一步，退到了状态： 。第一个空位上除了填过的 1，2，还可以填 3。第一个空位上填写 3，填写后为：3 __
填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：3 1 __
填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为：3 1 2
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。
因此再往后退一步，退到了状态：3 。第二个空位上除了填过的 1，还可以填 2。第二个空位上填写 2，填写后为：3 2 __
填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：3 2 1
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，2，没有其他数字可以填。
因此再往后退一步，退到了状态：3 。第二个空位上除了填过的 1，2，没有其他数字可以填。
因此再往后退一步，退到了状态： __。第一个空位上除了填过的 1，2，3，没有其他数字可以填。
此时深度优先搜索结束，输出了所有的方案。
算法：
- 用 path 数组保存排列，当排列的长度为 n 时，是一种方案，输出。
- 用 state 数组表示数字是否用过。当 state[i] 为 1 时：i 已经被用过，state[i] 为 0 时，i 没有被用过。
- dfs(i) 表示的含义是：在 path[i] 处填写数字，然后递归的在下一个位置填写数字。
- 回溯：第 i 个位置填写某个数字的所有情况都遍历后， 第 i 个位置填写下一个数字。
代码
#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{
if(u > n)//数字填完了，输出
{
for(int i = 1; i <= n; i++)//输出方案
cout << path[i] << " ";
cout << endl;
}
for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
{
if(!state[i])//如果数字 i 没有被用过
{
path[u] = i;//放入空位
state[i] = 1;//数字被用，修改状态
dfs(u + 1);//填下一个位
state[i] = 0;//回溯，取出 i
}
}
}
int main()
{
cin >> n;
dfs(1);
}
时间复杂度为 O(n*n!)。
空间复杂度为 O(n)。
有问题直接评论即可，
求点赞~谢谢
个人理解，递归就是实现位数之间的横向移动，遍历就是实现每一位上的纵向移动，两者结合就是全排列。有多少位，就有多少层，所以这个需要把数字竖过来放去想象dfs的搜索树结构，会更直观一点
你是不是说错了，递归是纵向的，往树的深处走，for循环才是横向移动。
+1
对诶
不是呀，你把数字竖起来，树的深处不就是数字的位数嘛，for循环是树的横向移动，是这个位数字的改变（这里再形象一点一个for循环就像一把数字密码锁）
对的
说白了 是看的参考系不同 人家是从树的结构来看 你是从数字竖起来看了 本质是一样的 建议按照自己手动模拟出来的树的结构去看吧
我知道他和你是什么意思
建议手动模拟一遍，注意for里面的i是多少，退出dfs不仅靠return,循环结束即意味着函数结束.
感谢大佬，大一学生手动模拟并理解。
%%% 感谢 之前没注意i 现在一眼手动模拟就悟了
谢谢大佬提醒 之前没注意 respect
n=3,第一次搜索出123一种方式，怎么回溯，继续进行啊，不懂？
s[3]=0,这时回到for循环，因为s[3]=0,所以dfs(2)成立，p[2]=3,这时就变成了1，3，2
走到了s[3]那不是再加1就跳出循环了函数结束了，为什么还要dfs[2]
感谢大佬，手动模拟一遍就悟了
同问？？
就是说：回溯时循环没结束，进行循环，循环结束时，往上一层回溯。
这是关键！
卡这了谢谢
请问bool类型的数组不初始化就默认都为FALSE吗？
全局变量是
好的，谢谢
思路完全理解，但是深究代码，还是觉得 不完全理解，输出一种方案后，例如输出1，2，3后，代码中如何实现回溯的？
for循环里面dfs调用结束之后，返回dfs这地方，继续执行dfs的下一条语句，再加上外面的for循环，要从1到3，完成回溯的。
回溯操作在return，return完这个递归就结束了，然后恢复现场，而你看懂没，这个u是一直没变过的，这样也就保证我每次都是从头开始遍历，我函数结束的条件就是for循环结束，也就是说for循环的作用其实就是开个排列的头，举个例子就是我for循环开头1，就从1开始递归下去，知道我把1到n个数都找完，也就是我把位子都填满，这个递归才会结束，但是这个递归还会返回上一层，比如1234返回，然后就1243，比较抽象，这个过程，也就是我填完4的时候，他会到递归到下一个位子，然后再来一遍循环，找到3填上去，然后输出，这个循环结束，然后再找到上面的循环，也就是13开头了，然后再往下走再遍历一遍找到2，然后再往下走.....
感谢感谢，我已经懂了，是回溯到for循环中去了，一开始没懂，感觉还是递归没有完全吃透。
感谢感谢，现在已经懂了，之前不懂还是因为递归没完全理解，总是不知道回溯到哪一步，现在完全明白了。
一直写法是u+1而不是u++,u本身不变，然后数组一直被覆盖就输出了
个人理解，递归就是实现位数之间的横向移动，遍历就是实现每一位上的纵向移动，两者结合就是全排列。有多少位，就有多少层，所以这个需要把数字竖过来放去想象dfs的搜索树结构，会更直观一点
为啥感觉输出1，2，3之后，dfs执行下一步就是state[3]=0；循环也结束了，然后呢？程序咋走？
同问
然后逐个退出函数，逐个恢复现场，直到最初那个选择第一个位置的函数，然后循环继续选择2
st[3] = false后，返回到st[2]的状态，因为当dfs(2)时，dfs下面的st[i + 1]也就是st[2]并没有执行，所以当st[3] = false时，退出dfs(3),返回到st[2] = false,这时发现i = 2,n = 3，i还可以 ++,所以i=3放在了第二位。
跳出当前函数
dfs(3)，回到上一层执行上一层dfs(2)中未执行完的代码。可以仔细看看递归的内容。我想问下为什么不需要在if(u>n)里return呢
return 也对，因为当u>n的时候，各个位置都填上了，所以走到for循环，里面的if都是假，然后程序就结束了。
在它要结束的时候那个for循环会回溯到3，然后再i++，变成4,根本进不去for循环，而且它此时的dfs函数也没有任何可以做的其他程序了，所以这儿不需要（u>n）也能结束dfs这个函数的。
每次再当前的格子(u)附上值,递归u+1，要记住u是不会变的，然后for循环致使是不断向前只有递归的时候才会从头算起，
是的，u是不变的
想问一下，这个的时间复杂度是怎么计算的呀？$输出时要遍历n个数，这里是O(n)，然后全排列一共有n!种状态，这里是O(n!)，然后每个状态都要输出一次，所以是O(n∗n!)。$
谢谢
伪代码展开123便于理解：
#include[HTML_REMOVED]
using namespace std;
const int N=10;
int path[N];
int state[N];
int n;
void dfs(int u)
{
// 当前递归深度达到n时，输出路径
if(u>n){
for(int i=1;i<=n;i++){
cout<<path[i]<<” “;
}
cout<<endl;
// 此时返回到上一层递归
return;
}
}
int main(){
cin>>n;
dfs(1);
}
看了一晚上终于悟了
确实不好理解啊
return是回到了那一步呢？直接退出dfs循环了还是回到了循环的开始呢？
可有可无
结束当前
dfs（u)的函数调用，回到上一层dfs函数中，执行上一层函数调用未执行的代码state[i] = 0,此时u也变成上一层函数调用的u
for循环里面的i如何变化？
666666
从123到132我已经想清楚了，但是现在想不明白132怎么变到2开头的数，132退回一开始三位全空的时候1、2、3都是false（未占）啊，怎么最高位就能变到2了呢
我也是不懂在评论区找答案，然后我现在自己想通了，就是跟你123到132一样的，回溯回去了是继续i，回到开头的时候i=1已经用了，i就是2开头了，就是下面说的每次dfs出来之后for里面的i是没变的不用从头开始，而是在原基础上继续
可以用vscode debug的方式看着他跑一遍，我看完一边后就能非常理解了
哇我也是按照代码做递归，直到我发现这个竟然和dfs的图完全吻合，应该先看那个树状图，再研究代码
https://www.bilibili.com/video/BV1kU4y1h77M/ 图解解释回溯看完应该有所帮助
链接里提到了两种写法，排列组合的另一种，能给出来吗？没成功：（
判断1时，1未被填写过，此时的u有数值吗,还是u是第一层的意思吗？代码中没有说明u是干嘛的不太清楚，大佬可以讲解一下吗
我的写法和你一样，但是我VS上报错，他说判断这个数字是否使用过的这个数组下标必须是指针类型。原话是表达式必须包含指向对象的指针类型，但它具有类型的int
回溯一直理解不了，在回退的同时还能保证u和i的对应关系，想不通一句代码就可以实现
可以把dfs直接展开写进代码里，试一试