换根DP

Description：
给定一颗 $n$ 个节点，$n - 1$ 条边的树
给定一个 guesses ：存储对某些节点的从属关系的猜测 [ u是v的父节点 ]
猜测哪些节点可以成为树的根，使得其为根的树至少满足 guesses 中的 $k$ 条从属关系

0x3f Tutorial

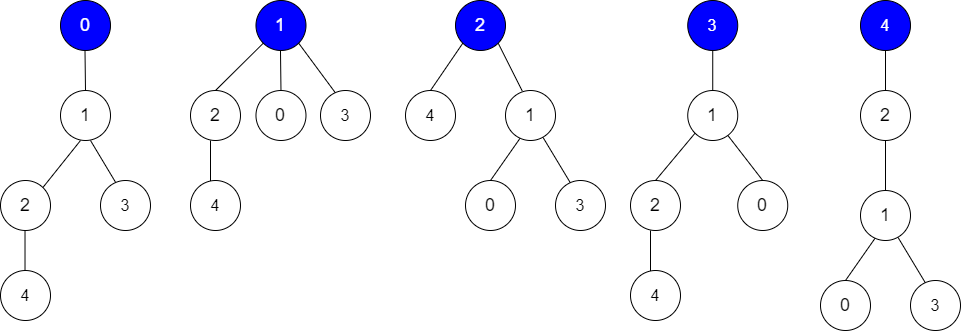
换根DP原理：

假设以 $x$ 为根的树的猜对次数为cnt，且存在一条根 $x$ 的子节点 $y$ 对应的边：$x \rightarrow y$，那么如果换成以 $y$ 为根，所有边的从属关系只有 $x \rightarrow y$ 会改变，其余都不会改变 [ 观察不难得到 ]，因此换根的时候只需要重新统计一条边即可 [ 快速判断是否有边可以用哈希表 ]

步骤：

1. dfs1：计算以 $0$ 为根的树对应的猜对次数：cnt —— 自项向下信息
2. dfs2：对应cnt的变化：cnt - (0, 1) in S + (1, 0) in s ( 换成以 $1$ 为根 )：观察状态转移方程，不难发现也是自项向下信息

不难发现，两次dfs都是自项向下维护信息，因此换根DP的dfs逻辑 [ 自底向上还是自项向下 ] 不是固定的，与具体需要维护什么信息有关

其中对于 C++ 二元组哈希的方法：将二元组的两个 $4$ 字节数字压缩成一个 $8$ 字节数字

<x, y> -> S

unordered_set<long> S;
S.insert((long) x << 32 | y); // 将两个 4 字节数字 压缩成 8 字节数字

//原理： 由于每一个数字都是唯一的，因此不同的二元组之间转化为数字不会冲突！

或是转化为 $N$ 进制

<x, y> -> (int)(x * N + y)

( 其中 $N$ 取 $131, 13331$ 类似哈希 )

C++ Code

class Solution {
public:
    int rootCount(vector<vector<int>> &edges, vector<vector<int>> &guesses, int k) {
        vector<vector<int>> g(edges.size() + 1);
        for (auto &e : edges) {
            int x = e[0], y = e[1];
            g[x].push_back(y);
            g[y].push_back(x); // 建图
        }

        unordered_set<long> S;
        for (auto &e : guesses) // guesses 转成哈希表
            S.insert((long) e[0] << 32 | e[1]); // 两个 4 字节数压缩成一个 8 字节数

        int ans = 0, cnt0 = 0;
        function<void(int, int)> dfs = [&](int x, int fa) {
            for (int y : g[x])
                if (y != fa) {
                    cnt0 += S.count((long) x << 32 | y); // 以 0 为根时，猜对了
                    dfs(y, x);
                }
        };
        dfs(0, -1);

        function<void(int, int, int)> reroot = [&](int x, int fa, int cnt) {
            ans += cnt >= k; // 此时 cnt 就是以 x 为根时的猜对次数 [ 初始的时候 x 表示已经计算完的 0 号点，随后从 0 号点逐步向其子节点转移 —— 递归的做 —— 自项向下 ] 
            for (int y : g[x]) // 遍历 x 的所有邻边
                if (y != fa) {
                reroot(y, x, cnt
                - S.count((long) x << 32 | y) // 原来是对的，现在错了
                + S.count((long) y << 32 | x)); // 原来是错的，现在对了
                }
        };
        reroot(0, -1, cnt0);  // 从 0 开始遍历
        return ans;
    }
};

Python3 Code

class Solution:
    def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:
        # 建图
        g = [[] for _  in range(len(edges) + 1)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        s = {(x, y) for x, y in guesses} # 哈希表  Py3 中 二元组可以哈希
        # Java C++ 或者将二元组映射为 long 数字 set<long> add((long)x << 32 | y)
        # Go pair{x, y int}  Go 语言可以直接二元组哈希

        cnt0 = 0
        def dfs(x: int, fa: int) -> None:
            nonlocal cnt0
            for y in g[x]:
                if y != fa:
                    if (x, y) in s:
                        cnt0 += 1  # 自项向下信息
                    dfs(y, x)
        dfs(0, -1)

        ans = 0

        def reroot(x : int, fa: int, cnt : int) -> None:
            # cnt 表示以 x 为根对应的猜对次数
            nonlocal ans
            if cnt >= k:
                ans += 1
            for y in g[x]:
                if y != fa:
                    reroot(y, x, cnt - ((x, y) in s) + ((y, x) in s))
        reroot(0, -1, cnt0)
        return ans