推荐题解

#include <iostream>
#include <cstring>

using namespace std;

const int N = 12, M = 1 << N; //M: 一共有多少种状态

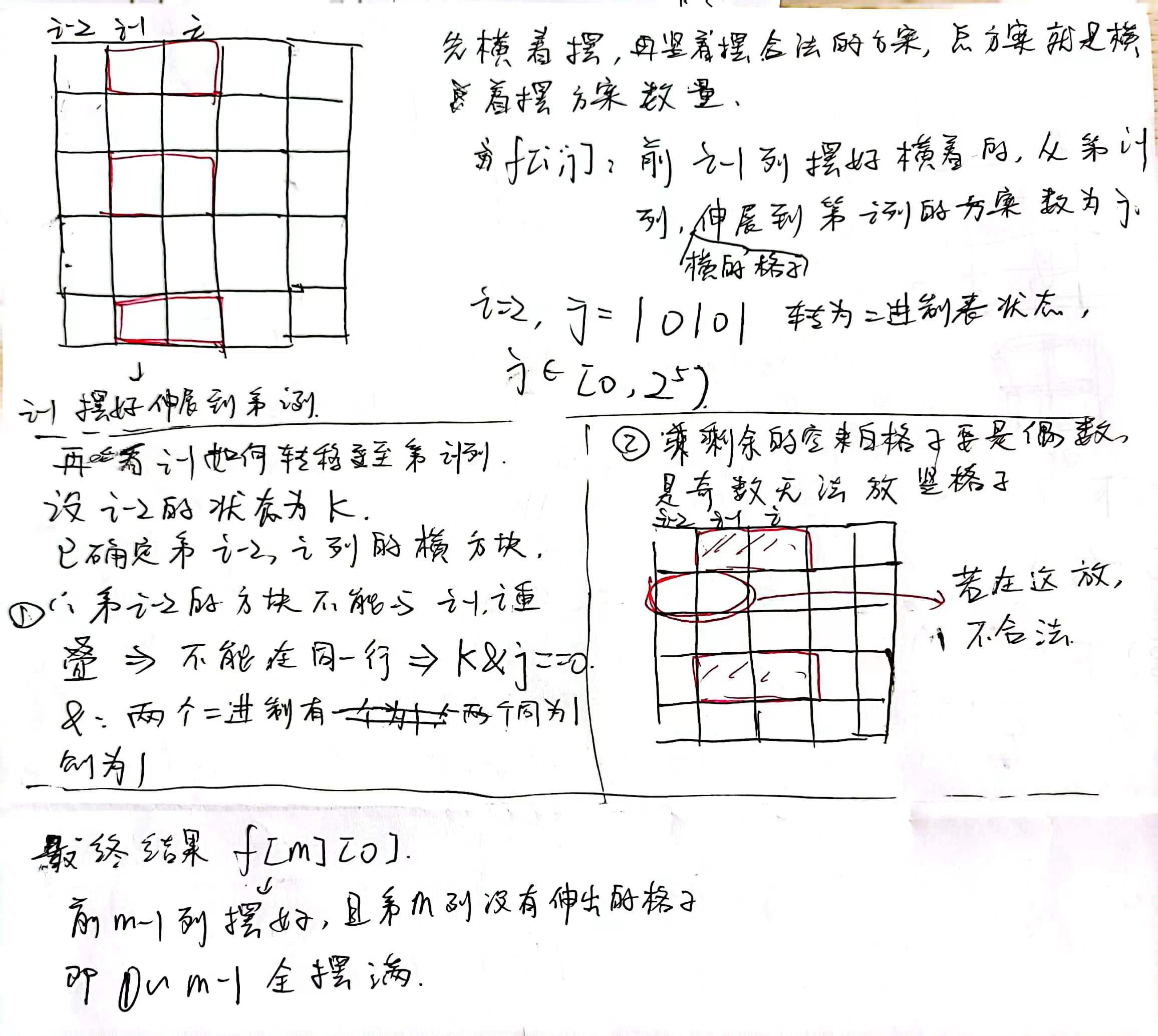
long long f[N][M]; //可能爆int，f[i][j]:摆好前i-1 列，第i-1 列状态是j，第i-1 列的横放格子延伸到第i 列。
bool vi[M]; //判断每一列哪些状态合法，要满足两个条件：i-2列与第i列不会冲突; 连续空格数量为偶数
int n, m;

int main()
{
    while (cin >> n >> m, n || m)
    {
        //枚举每一列的所有状态，找合法的状态
        for (int i = 0; i < 1 << n; i++) //状态数量为 2^n， n位二进制
        {
            int cnt = 0; //记录连续0 （空格）的数量
            vi[i] = true; //假设这个状态合法，找矛盾
            for (int j = 0; j < n; j++) //n 位二进制，从低位看
            {
                if (i >> j & 1) //若这一位是1
                {
                    if (cnt & 1) //若前面连续0的数量是奇数
                        vi[i] = false; //状态不合法
                    cnt = 0; //清空前面记录的连续0
                }
                else //这一位是0
                    cnt++;
            }

            if (cnt & 1) 
                vi[i] = false;
            /*
                判断开头处的连续0是否为奇数,我们还要看前导0是不是偶数
                如0001，要枚举完。
                我们右移的时候移的是n 位，可能最高位是0， 不是1.
            */
        }

        //多次输入，初始化
        memset(f, 0, sizeof f);
        f[0][0] = 1; //初始化

        //dp
        for (int i = 1; i <= m; i++) //从第一列开始
            for (int j = 0; j < 1 << n; j++) //枚举第 i 列的所有状态
                for (int k = 0; k < 1 << n; k++) //枚举第 i-1列的状态，第i-1 列状态也是第 i 列的伸出状态
                    if ((j & k) == 0 && vi[j | k])
                        f[i][j] += f[i-1][k]; 

        /*
             j&k == 0，i列与i-1列之间的状态没有冲突；
             j|k：两者有一个为1都为1。i-1的状态k 如何，i-1列会伸展到第i列，且已经保证了不冲突，所以 j&k 就是
                    第i列最终的状态，vi[j|k] = true, 表明状态合法
             f[i][j] += f[i-1][k] : 加上前一列，且第i-1列状态就是k 的方案数量
        */

        cout << f[m][0] << endl; //前m-1列已经摆好了，且第m 列没有伸出。即0~m-1列已经摆满了
    }

    return 0;
}