AcWing 1091. 理想的正方形【二维滑动窗口模型】    原题链接    中等

作者： 作者的头像   一只野生彩色铅笔 ,  2021-09-23 22:40:37 ,  所有人可见 ,  阅读 3265

38


6

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一个 $a \times b$ 的 矩阵 $w$，以及一个 正整数 $n$（其中 $w_{i,j}$ 为第 $i$ 行第 $j$ 列元素的 价值）

求 矩阵 $w$ 中，边长 为 $n$，且元素 最小最大值的差值最小 的 子矩阵，输出该 差值

分析

看到 区间最值 问题，第一反应是 预处理 st表，做一遍 二维RMQ

RMQ 本身是用于处理 多组询问 的，而本题则是要把所有 恒定边长 的 区间最值 找出来

介于只用维护 恒定边长，因此没有必要上 RMQ，但是 RMQ 的 思想 可以继承过来

考虑求一个 二维 的 最值问题，我们可以把它转化为一维 的 最值问题：

图中 红色阴影 格为该 行中 的 最值元素，绿色背影色 格为整个矩阵的 最值元素

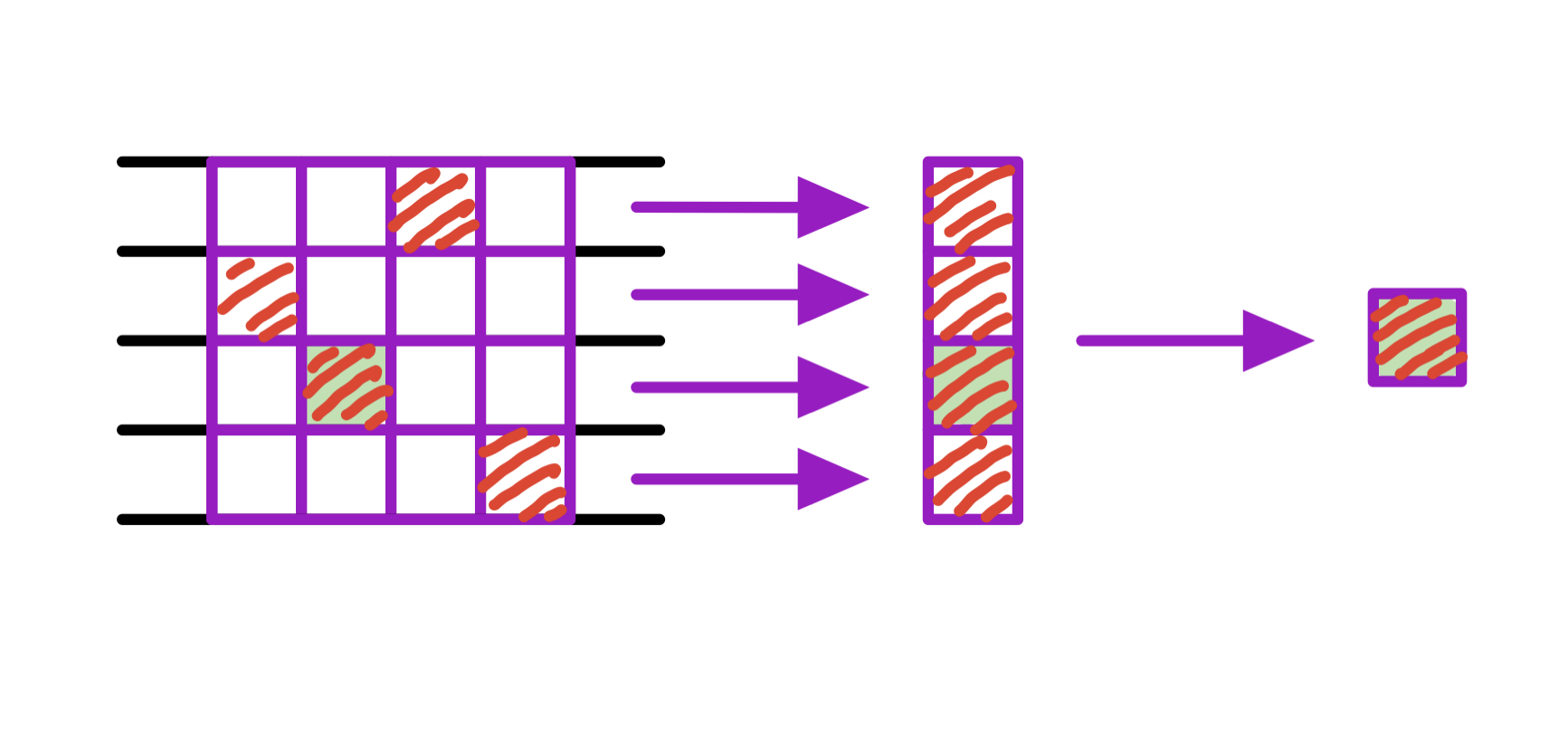
IMG_FFCE91A04185-1.jpeg

由常见公式 $\max\Big\{a,b,c,d\Big\} = \max\Big\{\max(a,b), \max(c,d)\Big\}$ 可知：

我们可以预处理出每 列 的行中 最值，再对该列求一个 最值，就是该 子矩阵 的 最值

该 降维手段，使得一个 二维滑动窗口问题 变成了 n行+n列 的 一维滑动窗口问题

而 一维滑动窗口 我们可太熟悉了，直接套 单调队列 的模板即可

所以这题和 动态规划 有什么关系吗 QAQ

Code

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, k, res = 1e9;
int w[N][N], minv[N][N], maxv[N][N], que[N];
int a[N], b[N], c[N], d[N];

void get_max(int a[], int f[], int m)
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= m; i ++ )
    {
        while (hh <= tt && i - que[hh] >= k) hh ++ ;
        while (hh <= tt && a[i] >= a[que[tt]]) tt -- ;
        que[ ++ tt] = i;
        f[i] = a[que[hh]];
    }
}
void get_min(int a[], int f[], int m)
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= m; i ++ )
    {
        while (hh <= tt && i - que[hh] >= k) hh ++ ;
        while (hh <= tt && a[i] <= a[que[tt]]) tt -- ;
        que[ ++ tt] = i;
        f[i] = a[que[hh]];
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &w[i][j]);
    for (int i = 1; i <= n; i ++ )
    {
        get_min(w[i], minv[i], m);
        get_max(w[i], maxv[i], m);
    }

    for (int i = k; i <= m; i ++ )
    {
        for (int j = 1; j <= n; j ++ )
        {
            a[j] = maxv[j][i];
            b[j] = minv[j][i];
        }
        get_max(a, c, n);
        get_min(b, d, n);
        for (int j = k; j <= n; j ++ ) res = min(res, c[j] - d[j]);
    }
    printf("%d\n", res);
    return 0;
}

19 评论

用户头像
lsp_同学   6个月前      1    踩      回复

这个图好形象呀！

用户头像
cocoshe   2023-04-27 03:40      1    踩      回复

我试了下deque，用deque实现是会被卡时间嘛？好像TLE了

用户头像
cocoshe   2023-04-27 03:41         踩      回复 
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1010;

int n, m, k, a[N][N];
int row_min[N][N], row_max[N][N], b[N], c[N], d[N], e[N], ans=1e9;
deque<int> q;

void get_min(int a[], int row_min[], int m) {
    q.clear();
    for (int i = 1; i <= m; i ++ ) {
        if (q.size() && i - q.front() >= k) q.pop_front();
        while (q.size() && a[i] <= a[q.back()]) q.pop_back();
        q.push_back(i);
        row_min[i] = a[q.front()];
    }
}

void get_max(int a[], int row_max[], int m) {
    q.clear();
    for (int i = 1; i <= m; i ++ ) {
        if (q.size() && i - q.front() >= k) q.pop_front();
        while (q.size() && a[i] >= a[q.back()]) q.pop_back();
        q.push_back(i);
        row_max[i] = a[q.front()];
    }
}

int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= m; j ++ ) {
            cin >> a[i][j];
        }
    }

    for (int i = 1; i <= n; i ++ ) {
        get_min(a[i], row_min[i], m);
        get_max(a[i], row_max[i], m);
    }

    for (int i = k; i <= m; i ++ ) {
        for (int j = 1; j <= n; j ++ ) {
            b[j] = row_min[j][i];
            c[j] = row_max[j][i];
        }
        get_min(b, d, n);
        get_max(c, e, n);

        for (int j = k; j <= n; j ++ ) 
            ans = min(ans, e[j] - d[j]);

    }
    cout << ans << endl;


    return 0;
}
用户头像
流动的音符   2023-08-19 15:40    回复了 cocoshe 的评论      1    踩      回复

你的代码+ (o)3优化就过了

用户头像
AcKing.   2021-09-27 16:53      1    踩      回复

巨巨，我想请教一下。
for (int i = 1; i <= m; i ++ ) { while (hh <= tt && i - que[hh] >= k) hh ++ ; while (hh <= tt && a[i] >= a[que[tt]]) tt -- ; que[ ++ tt] = i; f[i] = a[que[hh]]; }
这个get_max里面，把最后一行移到第二行之前，就报错呀？

用户头像
一只野生彩色铅笔   2021-09-27 17:02      3    踩      回复

$j$ 的范围应该是：$0 \le i-j \lt k$，所以求 $i$ 的最值时，要先把 $i$ 滑进当前的滑动窗口

具体一点来理解的话，计算以第 $i$ 哥元素为 右端点 的最大值，要算上第 $i$ 个元素

用户头像
一只野生彩色铅笔   2021-09-27 17:04      2    踩      回复

这个分析也适用所有的 滑动窗口模型 问题

如果 $1 \le i - j$ 就要先算，再加

如果 $0 \le i - j$ 就要先加，再算

用户头像
AcKing.   2021-09-27 18:59    回复了 一只野生彩色铅笔 的评论         踩      回复

感谢大佬指点！！！十分通透

用户头像
AcKing.   2021-09-27 16:19      1    踩      回复

题解很清晰，彩铅大佬tql！！！

用户头像
一只野生彩色铅笔   2021-09-27 17:02         踩      回复

谢谢大佬的夸奖 w

用户头像
waydedie   2023-03-19 15:32         踩      回复

我不太理解关于tt=0和tt=-1有什么差别

用户头像
糖豆   2023-06-14 10:19      2    踩      回复

tt=0：表示提前入队列了一个哨兵，此种情况一般与前缀和共同使用，因为计算s[9]-s[0]，就是获取1~9的前缀和，此时提前入队列一个哨兵，保证了所有数据的处理逻辑一致，否则就会造成对于第1个数据，它的处理逻辑与其它的不一致.
tt=-1：这是基础课中队列的标准姿势，就是普通的队列，没有加入哨兵。因为本题没有涉及到前缀和概念，不需要什么哨兵，而且，通过观察法，你就能知道，主体代码在没有初始入哨兵时才是正确的。

用户头像
xyh2   2023-01-14 10:06         踩      回复

哈哈哈，牛逼大佬

用户头像
zshzsh   2022-11-05 15:37         踩      回复

二维降到一维的过程有详细点的文章吗

用户头像
陈平安   2021-10-03 22:21         踩      回复

佬，如果用minv[i][j]表示从(1,1)到(i,j)的最小值，行从k开始才是对的呢，从1开始就不对了呢，我是用一个二维数组minv[i][j]存储最大值，maxv[i][j]存储最大值，计算res是把单独提出了了。我的代码：
https://pastebin.ubuntu.com/p/2XChXt3bSq/
第51行标注了我的问题

用户头像
一只野生彩色铅笔   2021-10-03 23:36         踩      回复

注释的那一行改成 $1$ 也能过，不影响答案的枚举，但是 $1\sim k-1$ 的迭代都是不合法答案

可以看一下上面有关二维滑动窗口化一维的思路

我们是把第一 列 合法的子窗口的 行中 最值存储到第 $k$ 列的单独元素中去

如果去迭代 $1\sim k-1$ 的列，是没有意义的，他们的实际意义是 $1\sim k-1$ 长的子矩阵

计算他们的时候 滑动窗口 未满

如果维护的 二维滑动窗口 要求是长宽不超过 $k$ 的话，那样才是正解

用户头像
陈平安   2021-10-04 07:50    回复了 一只野生彩色铅笔 的评论         踩      回复

明白了，谢谢大佬解答！

用户头像
Hygen   2021-09-24 00:04         踩      回复

巨巨这么晚还在写题解，我又有什么资格睡觉！

用户头像
一只野生彩色铅笔   2021-09-24 07:55         踩      回复

冲冲冲