最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划
题目描述
给定一个含有 $n$ 个结点的 树
每个结点有一个 权值 $w_i$ 表示在第 $i$ 个点上放置 哨兵 的 花费
对于每个 哨兵 来说，他可以 观察 当前结点，以及所有与当前点 相连 的 相邻结点
求解一种放置哨兵的 方案，使得每个 结点 都被 观察 到，且方案的 花费 最小
分析
本题是 AcWing 323. 战略游戏【树形DP+状态机模型】 的改版题
在 战略游戏 中，题目要求的放置方案是 每条边 都被 观察 到，而本题则是要求 每个点 都被 观察 到
因此我们还是同样使用 树形DP 来求解方案
本题的要求相对于 战略游戏 ，稍稍增加了一些 难度，原因如下：
如果只是要求 每条边 被 观察 到，那么我们在处理 父节点 时，枚举到一个 子节点 就可以直接进行讨论
- 父节点 放置 哨兵，所有子节点都 可放可不放 哨兵
- 父节点 不放 哨兵，所有子节点 都要放置 哨兵
但是在本题的 要求 中，每条边 变成了 每个点 就会出现如下三种情况：
- 父节点 放置 哨兵，所有子节点都 可放可不放 哨兵
- 父节点 不放 哨兵，但是他至少有一个 子节点 放置哨兵，观察住了他
- 父节点 不放 哨兵，但 父节点 的 父节点 放置哨兵观察，则 子节点 可放可不放 哨兵
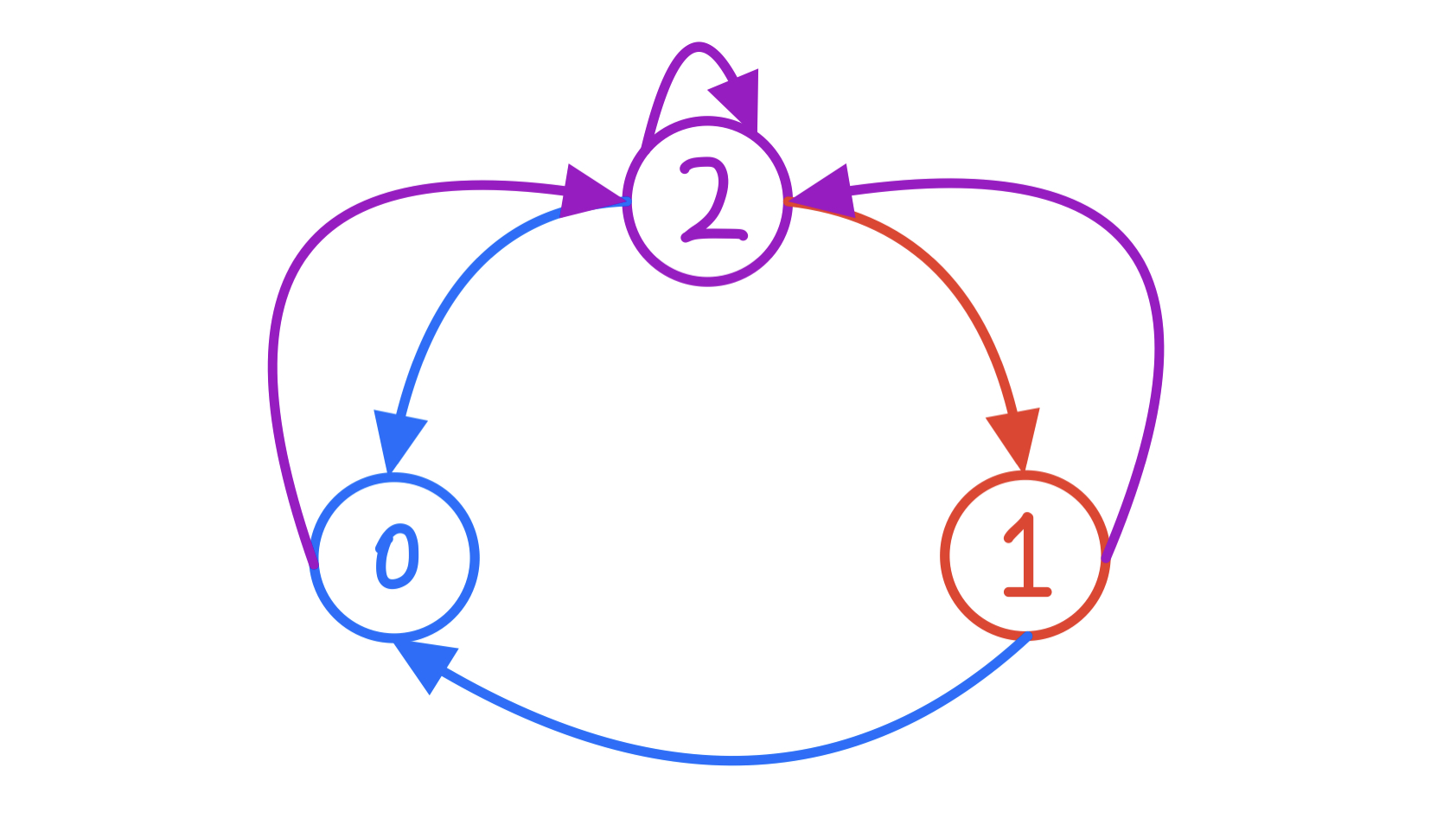
这样每个结点就有 三种情况 要转移，简略状态机模型如下：
- 被父节点观察 （0）
- 被子节点观察 （1）
- 被自己来观察 （2）
闫氏DP分析法
状态表示 — $f_{i,0/1/2}$ 集合： 以结点 $i$ 为 根节点 的子树，在 $i$ 状态为 $j$ 的方案
状态表示 — $f_{i,0/1/2}$ 属性： 方案中，放置哨兵的代价 最少
状态计算：
在 $i$ 上被父节点观察 （0）：
$$ f_{i,0} = \sum_{i_{ch}} \min(f_{i_{ch}~,1}, f_{i_{ch}~,2}) \\\ i_{ch} \in \{ver | ver\text{是 i 的子节点}\} $$
在 $i$ 上被子节点观察 （1） ：
$$ f_{i,1} = \min(f_{i_{ch}~,2} + \sum_{other~i_{ch}}\min(f_{other~i_{ch}~,1}, f_{other~i_{ch}~,2}))\\\ i_{ch} \in \{ver | ver\text{是 i 的子节点}\} \quad other~i_{ch} \in \{ver | ver\text{是 i 的子节点，且 }ver \ne i_{ch} \} $$
在 $i$ 上被自己来观察 （2） ：
$$ f_{i,2} = \sum_{i_{ch}} min\big\{{f_{i_{ch}~,0}, f_{i_{ch}~,1}, f_{i_{ch}~,2}}\big\} + w_i\\\ i_{ch} \in \{ver | ver\text{是 i 的子节点}\} $$
Code
时间复杂度： $O(n)$
#include <iostream>
#include <cstring>
using namespace std;
/*
以下注释为早期笔记，希望对你有所帮助
状态机 + 树形Dp问题
状态表示:
f(i, 0)：第i号结点被他的父结点安排的守卫看住的方案数
f(i, 1)：第i号结点被他的子结点安排的守卫看住的方案数
f(i, 2)：第i号结点自己安排守卫看住的方案数
状态计算:(j是i的子结点)
f(i, 0) = sum{min(f(j,1), f(j,2))}
i是被他父结点看住的，那他的子结点要么自己看自己，要么被自己的子结点看住
f(i, 1) = min{w(k) + f(k, 2) - sum{min(f(j,1), f(j,2))}}
i如果是被子结点看住的，那么就要枚举他是被哪个子结点看住的所有方案，对所有方案求最小值
这里的sum不包括j==k的情况，因此需要手动额外减去
f(i, 2) = sum{min(f(j,0), f(j,1), f(j,2))} + w(u)
i是被自己看住的，那他的子结点可以被父结点看住，可以自己看自己，也可以被自己的子结点看住
*/
const int N = 1510;
int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];
bool st[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
f[u][0] = 0;
f[u][1] = 1e9; //f[u][1]求最小值，初始化为最大值
f[u][2] = w[u];//初始化放置自己的代价
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
}
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
//f[u][0]中记录了sum{min(f(j,1), f(j,2))}，再从中减去对应的贡献即可得到remain ver
f[u][1] = min(f[u][1], f[u][0] + f[j][2] - min(f[j][1], f[j][2]));
}
}
int main() {
memset(h, -1, sizeof h);
cin >> n;
for (int i = 1; i <= n; ++i) {
int id, cnt, cost;
cin >> id >> cost >> cnt;
w[id] = cost;
while (cnt--) {
int ver;
cin >> ver;
add(id, ver);
st[ver] = true;
}
}
int root = 1;
while (st[root]) ++root;
dfs(root);
printf("%d\n", min(f[root][1], f[root][2]));
return 0;
}
写的好，状态机玩得明白
请问一下，这道题和上道题《战略游戏》很像，为什么这道题有三种状态，而上道题只有两种，二者不都是既可以被父节点影响，也可以被子节点影响吗，二者区别在哪里呀，麻烦大佬啦
但是题意不一样呀，战略游戏那题是看守的边，这题是看守的点
感觉可以这样解释：
战略游戏：需要保证所有的边都要被看到，所以如果父节点不选的话，那么子节点必须选，才能保证所有的边都能被看到。
皇宫看守：只要保证所有的点被看到即可，所以如果父节点不选的话，那么只需要保证至少有一个子节点被选到即可
请问式中当前节点的贡献为啥是
min(f[j][1], f[j][2])枚举的时候不是把当前节点设为f[j][2]了吗其中
f[j][2] + f[u][0] - min(f[j][1], f[j][2])f[j][2]表达的是当前f[u][1]可以从子节点j放置守卫这一状态转移过来f[u][0] - min(f[j][1], f[j][2])表达的是其他(除j外)各个子节点最少可以放置守卫的数量因为:
$$ f[u][0]=\sum \min(f[k_i][1],f[k_i][2]) $$
$k_i$是u的子节点，
min(f[j][1], f[j][2])其实只是组成f[u][0]的一部分，所以f[u][0] - min(f[j][1], f[j][2])意为除当前节点j外，u的其他子节点在合法状态下最少放置守卫数量的最小值。希望能帮到你
明白了 谢谢你~
or2 or2
wok，你这个我一看明白了谢谢大佬
彩铅大大你的code f(i, 1) = min{w(k) + f(k, 2) + sum{min(f(j,1), f(j,2))}}
i如果是被自己点看住的，那么就要枚举他是被哪个子结点看住的所有方案，对所有方案求最小值
这里的sum不包括j==k的情况，因此需要手动额外减去
的“自己”字儿写错了，应该是子节点
而且还不是+sum(min(f[j][1],f[j][2]))应该是减去吧Orz
谢谢指出，已更正
f[u][1] = min(f[u][1], f[u][0] + f[j][2] - min(f[j][1], f[j][2]));大佬们这个是怎么得出来的啊
还是得讨论清楚再写代码……。瞎搞不好……
我知道我代码的问题了， 我仅被父节点观察到的状态dp[curr][0] 是不能从子节点放置了卫兵转换过来的 dp[son][2]。 只能从dp[son][1]转换。 所以多了很多处理.
想问一下根节点它的f[root][0]是怎么被算的，既然f[root][0]不存在，为什么不是正无穷啥的呢
f[u][1]为什么要单独再开一个for来求，为什么不能直接在第一个for里面同时求f[u][0]、f[u][2]和f[u][1]?
这个问题我也糊涂过，现在来解释一下：
注意第一个循环中的写法：
这是在枚举每个u的儿子j,然后把j儿子自己放守卫，j儿子指望它的某个儿子看守望的情况两者的最小值进行累加，最终形成累加和sum=d[u][0],注意,是最终的累加和啊！！！也就是所有儿子v1,v2,v3,…的取值累加和。
在第二个循环中，我们期望如果现在指望 j儿子给u守卫的话，那么f[j][2]是肯定要付出的代价，那其它儿子需要付出的整体代价就是sum-min(f[j][1],f[j][2])! 注意：这里的是sum!!!
如果我们把三个状态转移全部放在第一个循环中，我们就会发现，当我们需要全部的累加和sum时，上面的f[u][0]还没有加完毕！！还只是一部分儿子j的sum和，并不是全部，而我们要全部的sum和，这就意味着我们需要等待上面的所有j累加完，也就是执行完一遍循环后，才能拿到这个需要的sum值，这就解释了为什么要用两遍循环的原因。
巨巨注释是不是写错了
f(i, 1) = min{w(k) + f(k, 2) - sum{min(f(j,1), f(j,2))}}应该是
f(i, 1) = min{w(k) + f(k, 2) + sum{min(f(j,1), f(j,2))}}吧
减去的应该是当前枚举的到子节点
j的min{f(j,1),f(j,2)}没错，你看下下面 “那颗白杨树 “ 的评论就明白了。
%%%%%
Orz
f[u][1] = min(f[u][1], f[u][0] + f[j][2] - min(f[j][1], f[j][2]));
这一行好难理解,谁能再解释下
同问
我好像知道了，f[j][2] - min(f[j][1], f[j][2]这里就是求除了当前枚举的子节点之外其他的子节点的最小值
补充一下， 一开始是子节点全选，然后随着子节点的列举sum逐渐减小最后变成0表示只选了一个子节点K
emm,这行的意思表示的就是这个式子吧:
fi,1=min(fich ,2+∑other ichmin(fother ich ,1,fother ich ,2))
枚举u的子节点j, 在j上放哨兵 对应 f[j][2], f[u][0] - min(f[j][1], f[j][[2]) 表示∑other ichmin(fother ich ,1,fother ich ,2)，这两个式子等价是因为f[u][0]中记录了sum{min(f(j,1), f(j,2))}
是不是要建双向边
这题可以不建双向边。 建不建双向边取决于题目是否把父节点和子节点之间的关系告诉你， 因为我们最终只是建图做dfs，会确保树中的每个点只会遍历一次。 如果知道了父节点和子节点的关系，我们可以直接建有向图，但是需要用一个st数组找根。反之我们要建双向图，这样我们的起点可以从任意点开始，但是需要一个dfs(u, fa)需要传入它的父节点，确保每一个点只会遍历一次。
👍👍👍
%%%
%%%
彩铅大大，感觉状态机哪个图画错了，0 应该也可以连一条边到 1
彩铅 0 点写题解%
确实 QAQ
状态1表示：当前节点不放置哨兵，且当前节点被其子节点观察。相应地，该节点的子节点的状态可以是：放置哨兵，自己观察自己，即状态2；不放置哨兵，被它的子节点观察，即状态1。综上，状态1可以由状态1或2转移得到。0不能连一条边到1，而应该是1自己连一条边到自己。
既然其中一个子节点放的时候父节点不放，那为什么图中的 $1$ 状态可以转移到 $0$ 状态上？
也就是说，子节点的父节点不应该不放吗（）
这里是取了两个集合的交集一起转移的
即，子节点放，父节点不放；子节点放，父节点放
大佬 现在好像加强了数据代码TLE了
嗷嗷嗷没有没有，调试TLE，但是正式交就能过了
%%%%%%
题解写的越来越好了 Orz
谢谢w
算当前节点被子节点看守住f[u][1]时，算法已经包含了多个子节点看守当前该结点吧？
是的，集合划分的时候相交是没问题的，只要不遗漏就好
明白了，谢谢！