历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1013. 机器分配【分组背包+背包DP输出方案—拓扑图分析】原题链接简单

作者：

一只野生彩色铅笔 , 2021-06-21 22:35:44 , 所有人可见 , 阅读 7105

113

50

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

总公司拥有 $M$ 台相同设备，准备分给下属的 $N$ 个分公司。

第 $i$ 家公司分到 $j$ 台机器后，所获的的收益为 $w_{ij}$

求一种分配方案，使得总收益最大，输出该方案

分析

本题乍一看很像是 背包DP，为了转换成 背包DP 问题，我们需要对里面的一些叙述做出 等价变换

每家公司 我们可以看一个 物品组，又因为 每家公司 最终能够被分配的 机器数量 是固定的

因此对于分给第 $i$ 个公司的不同 机器数量 可以分别看作是一个 物品组 内的物品

该物品 $k$ 的含义：分给第 $i$ 个公司 $k$ 台机器

该物品 $k$ 的体积：$k$

该物品 $k$ 的价值：$w_{ik}$

于是，本题就转换成了一个 分组背包问题

直接上 分组背包 的 闫氏DP分析法

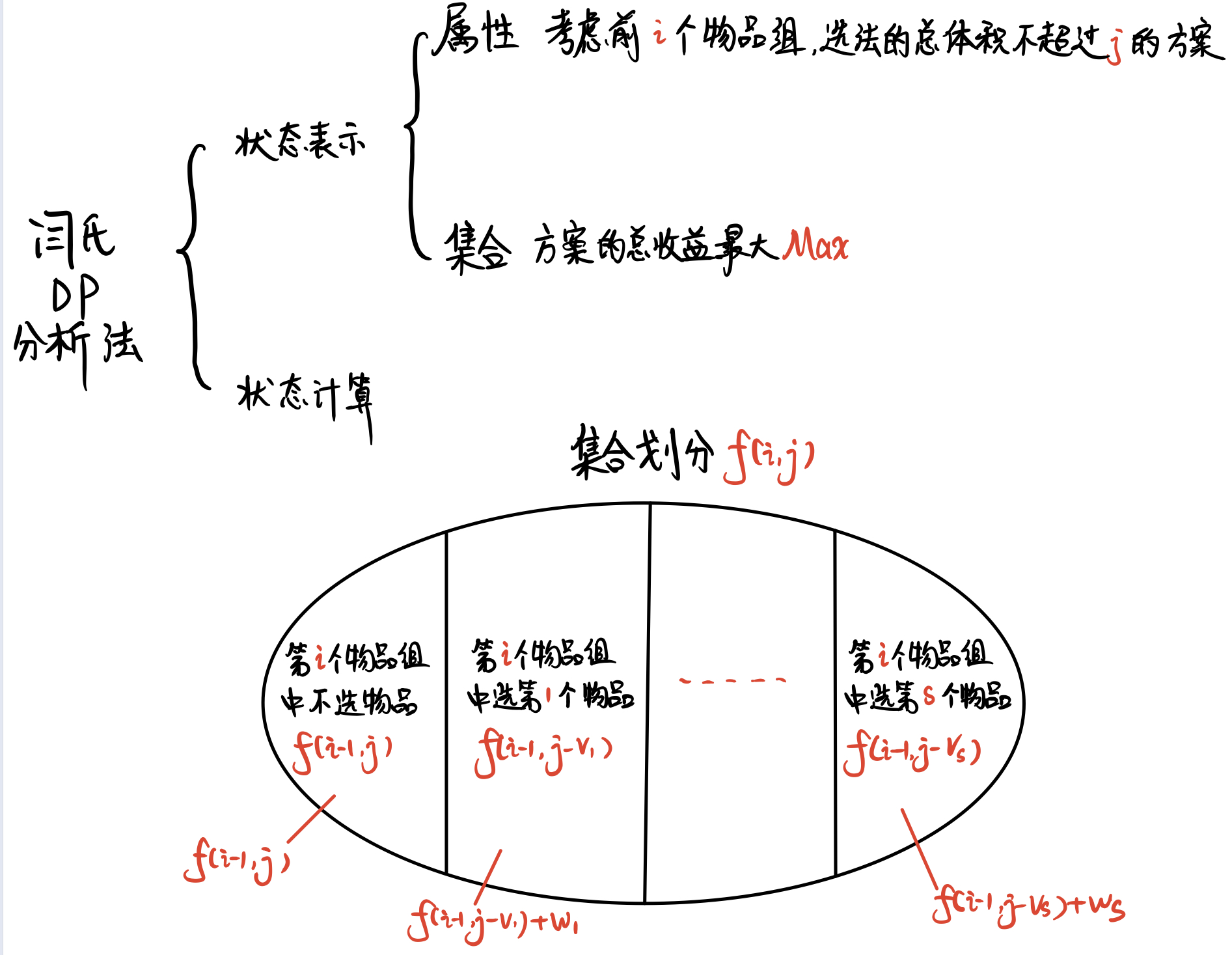
初始状态 ：f[0][0]

目标状态 ：f[N][M]

动态规划求状态转移路径

这里我介绍一个从图论角度思考的方法

动态规划 本质是在一个 拓扑图 内找最短路

我们可以把每个状态f[i][j]看作一个点，状态的转移 看作一条边，把 状态的值 理解为 最短路径长

具体如下图所示：

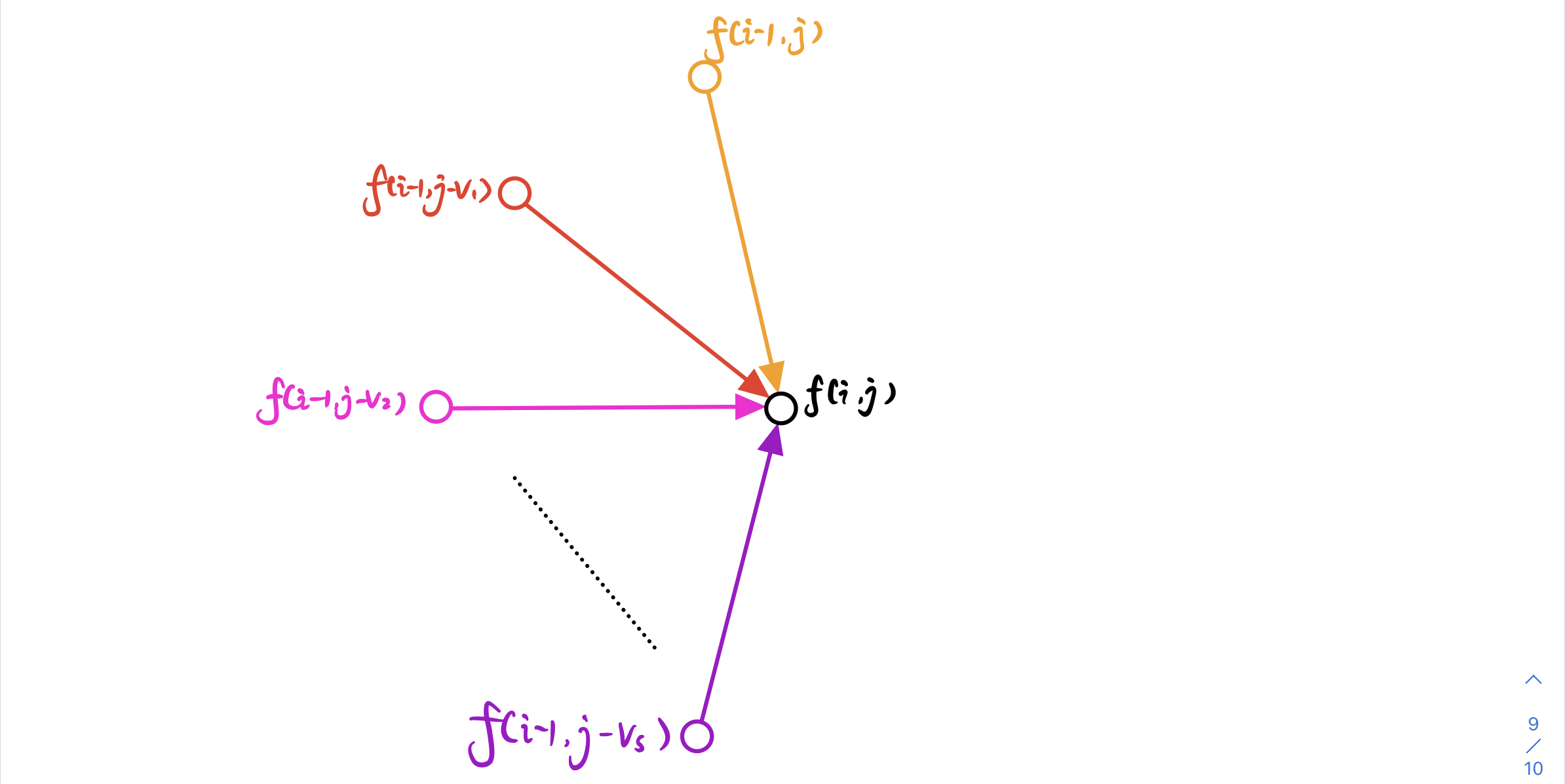
对于点 f[i][j] 来说，他的 最短路径长 是通过所有到他的边更新出来的

更新 最短路 的规则因题而已，本题的 更新规则 是 $f(i,j)=\max\{f(i-1,j-v_i)+w_i\}$

最终，我们会把从 初始状态（起点）到 目标状态 （终点）的 最短路径长 更新出来

随着这个更新的过程，也就在整个图中生成了一颗 最短路径树

该 最短路径树 上起点到终点的路径就是我们要求的 动态规划的状态转移路径

如下图所示：

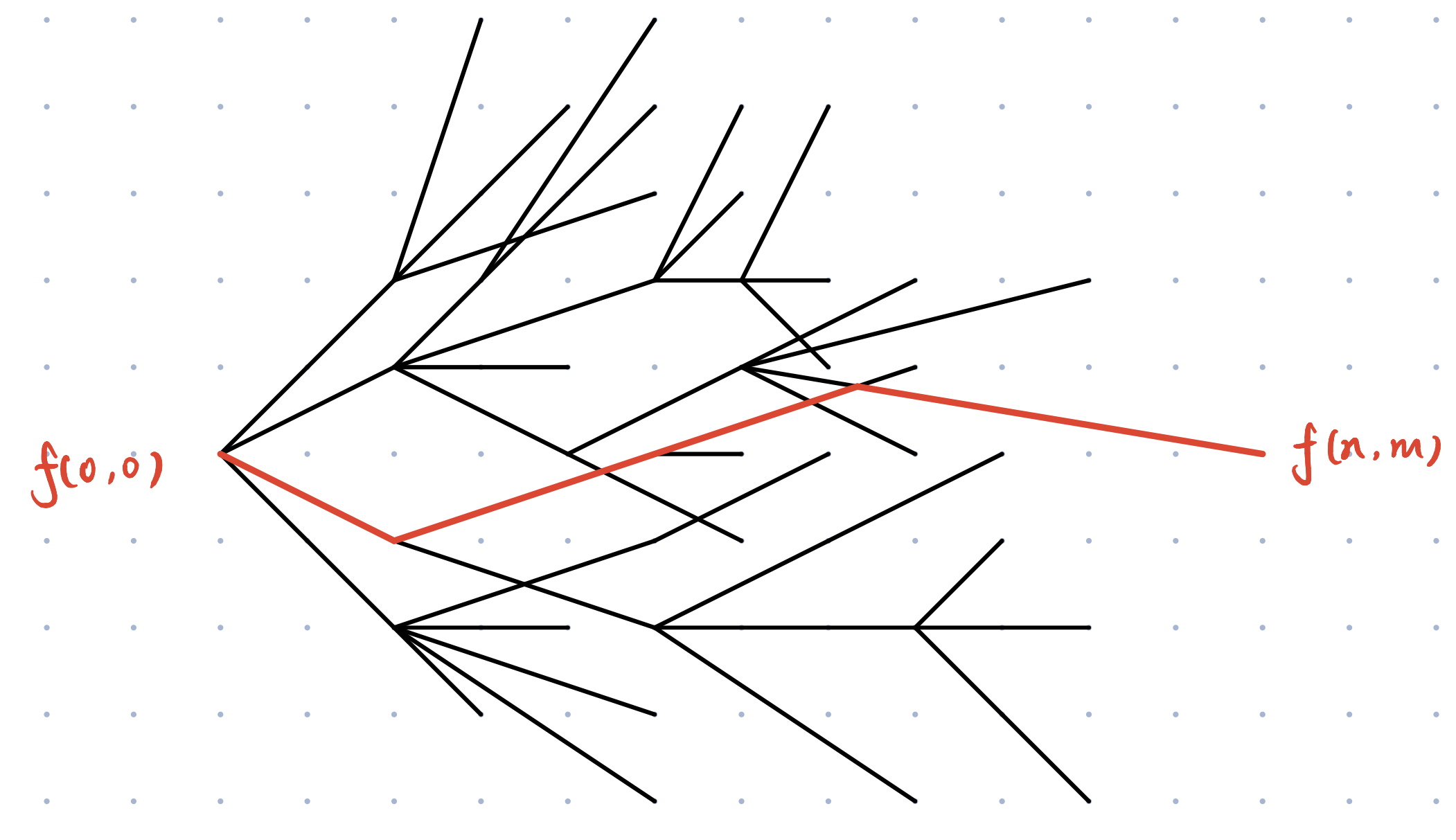
那么 动态规划求状态转移路径 就变成了在 拓扑图 中找 最短路径 的问题了

可以直接沿用 最短路 输出路径的方法就可以找出 状态的转移

Code

找 最短路径 递归写法

#include <iostream>

using namespace std;

const int N = 20;

int n, m;
int w[N][N];
int f[N][N];
int path[N], cnt;

void dfs(int i, int j)
{
    if (!i) return;
    //寻找当前状态f[i][j]是从上述哪一个f[i-1][k]状态转移过来的
    for (int a = 0; a <= j; ++ a)
    {
        if (f[i - 1][j - a] + w[i][a] == f[i][j])
        {
            path[cnt ++ ] = a;
            dfs(i - 1, j - a);
            return;
        }
    }
}
int main()
{
    //input
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
        for (int j = 1; j <= m; ++ j)
            cin >> w[i][j];

    //dp
    for (int i = 1; i <= n; ++ i)
        for (int j = 1; j <= m; ++ j)
            for (int k = 0; k <= j; ++ k)
                f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
    cout << f[n][m] << endl;

    //find path
    dfs(n, m);
    for (int i = cnt - 1, id = 1; i >= 0; -- i, ++ id)
        cout << id << " " << path[i] << endl;
    return 0;
}

28 评论

zad456 2021-09-12 07:46

妙啊，作者真他娘的是个人才！

farmerghost 7个月前

为什么最后是要倒序输出路径啊？？？

farmerghost 7个月前

是因为是从最终目标状态开始递归的吗？？

艾特玖 7个月前回复了 farmerghost 的评论

对的

baby_6 2023-08-28 07:50

闫氏dp分析法的集合和属性似乎反了

小小侠客 2022-08-15 20:45

一本通的那个第二个点我也错了

LingKerly 2023-01-11 15:53

测试点//input
2 15
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
测试点//output
2
1 0
2 15
dfs代码//output
2
1 1
2 1
special judge没写好吧

椎名まひる 2023-08-02 20:11 回复了 LingKerly 的评论

这题不要求字典序最小的，想要字典序最小倒着枚举就行

farmerghost 7个月前回复了 LingKerly 的评论

acwing上可以过

䦹徊 3个月前

Acwing的题解质量是其魅力之一

YAX_AC 4个月前

#include[HTML_REMOVED]
#include[HTML_REMOVED]

using namespace std;

const int N = 11,M = 16;

int n,m;
int w[N][M];
int f[N][M];
int path[N],cnt = 1;

void dfs(int i,int j)
{
if(!i) return;

//寻找当前状态f[i][j]是从哪一个f[i-1][k]状态转移过来的
for(int k = 0; k<=j; k++)
{
    if(f[i-1][j-k]+w[i][k] == f[i][j])
    {
        path[i] = k;
        cnt++;
        dfs(i-1,j-k);
        return;
    }
}

}

int main()
{
cin>>n>>m;

for(int i = 1; i<=n; i++)
    for(int j = 1; j<=m; j++)
        cin>>w[i][j];

for(int i = 1; i<=n; i++)//物品
    for(int j = 0; j<=m; j++)//体积
        for(int k = 0; k<=j; k++)//决策
            f[i][j] = max(f[i][j],f[i-1][j-k]+w[i][k]);
cout<<f[n][m]<<endl;
//找最短路
dfs(n,m);
for(int i = 1; i<cnt; i++) cout<<i<<' '<<path[i]<<endl;
return 0;

}

辞寒 9个月前

狠狠地点了，理解得很透彻~~

我真的菜死了 2023-05-07 15:08

666

2001f 2022-10-21 17:51

有些好奇，这种dfs的写法感觉和y总的写法是同一个意思，是会比y总那样找出答案路径更快一些吗？

Leonys 2023-08-03 20:04

时间复杂度应该是一样的

做ac梦w 2022-08-14 12:27

你好你的代码在一本通交wa了一个点

LingKerly 2023-01-11 15:53

测试点//input
2 15
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
测试点//output
2
1 0
2 15
dfs代码//output
2
1 1
2 1
special judge没写好吧

selfknow 2022-03-27 15:24

 // 每次一定是从上一个公司到这一个公司
    // 看看上一个公司用了几个机器才达到当前状态的
    for(int a=0;a<=j;a++)
        if(f[i-1][j-a]+w[i][a]==f[i][j])
        {
            path[i]=a;
            ++cnt;
            dfs(i-1,j-a);
            return ;

        }

dfs这样记录，输出会方便一点

糖豆 2022-07-26 10:54

建议这样：

void out(int i, int j) {
    if (i == 0) return; //走出界就完事了
    int k = path[i][j];
    out(i - 1, j - k); //利用递推的栈机制，后序输出，太强了~
    printf("%d %d\n", i, k);
}

//　调用示例：
for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++)
            scanf("%d", &w[j]);

        for (int j = m; j; j--)
            for (int k = 1; k <= j; k++) {
                int val = f[j - k] + w[k];
                if (val > f[j]) {
                    f[j] = val;
                    //在状态转移时，记录路径
                    path[i][j] = k;
                }
            }
    }
    //输出结果
    printf("%d\n", f[m]);
    //输出路径
    out(n, m);