历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 532. 货币系统【完全背包求解最大无关向量组个数】原题链接中等

作者：

一只野生彩色铅笔 , 2021-06-14 00:23:09 , 所有人可见 , 阅读 7035

131

34

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

定义一个 货币系统 $(n, a)$ ：一共有 $n$ 种货币，每种货币对应面值为 $a_i$

每种货币可以使用 任意多个，进行线性组合：

$k = x_1a_1 + x_2a_2 + \cdots + x_na_n，其中 x_i \in Z_0~~i=1,2,\cdots$

$k$ 为该 货币系统 $(n, a)$ 能够 线性表出 的数值

【注】本题的 线性表出 对于系数的要求和 线性代数 中的 线性表出 是不一样的

本题的系数必须是 非负整数

定义：
$(n, a) 和 (m, b) 等价 \Leftrightarrow \forall k \in Z^+， \begin{cases} k如果能被a线性表出，则k也能被b线性表出\\\ k如果不能被a线性表出，则k也不能被b线性表出 \end{cases}$

现给定 货币系统 $(n, a)$ ，求一个等价的 货币系统 $(m, b)$ ，要求 $m$ 尽可能最小

分析

$n$ 种货币，每种货币可以使用 无穷多个

通过这些信息，我们可以初步识别该题目是一个 完全背包 的变种题目

接着我们需要挖掘一下题目里的性质：

学过 线性代数 的同学可以无视这一部分，跳到下面的分割线继续看

研究 货币系统 $(n, a)$ ，如果存在 $a_j$ 可以被 $a$ 中其他的向量 线性表出：

$a_j = \sum_{i\ne j} c_ia_i$

则 $a_j$ 在这个货币系统中是 无效的 (所有线性表示中需要用到 $a_j$ 的项，都可以用 $\sum_{i\ne j} c_ia_i$ 代替)

因此，我们需要求出 货币系统 $(n, a)$ 的 最大无关向量组，即任意 $a_i$ 都不能被其他向量 线性表出

如何求向量组 $(a_1,a_2,\cdots,a_n)$ 的最大无关向量组

我们可以利用到数论中 埃式筛法 的思想：

对于一个 无效的 元素 $a_i$ ，他只会被小于他的元素的 线性组合 表出，满足该要求的 $a_i$ 就要被筛掉

所以我们要先排序

而我们在做 完全背包 的时候，需要求出所有恰好能被前 $i$ 个物品选出的体积的方案

即就是在 完全背包 求方案数的过程中，统计那些 初始不能被满足 的物品体积个数

这就是我们在 AcWing 1021. 货币系统中所使用的 DP模型

那一题我们求解的是方案数，这题稍微改一下，改成这种方案能否被满足即可，具体如下

闫氏DP分析法

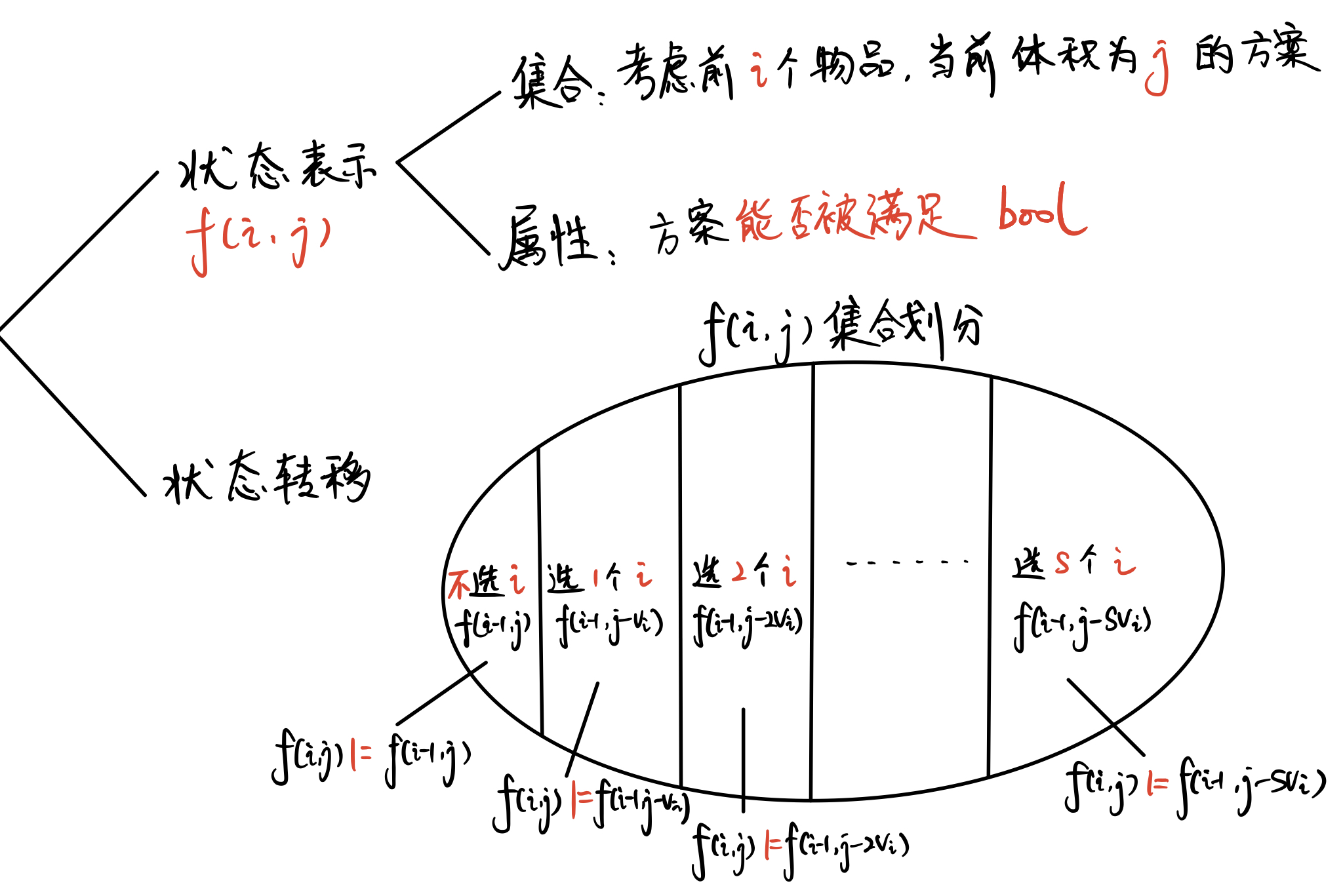
再具体一点的代码实现，我会在代码的注释中再具体解释

Code

时间复杂度： $O(n\times m)$

空间复杂度： $O(m)$

其中 $m$ 是最大物品的体积

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

//这题是一道线性代数问题
//求解一个向量组的秩(最大无关向量组的向量个数)
//但是代码写起来就是一个模拟筛的过程
//从小到大，先查看当前数有没有被晒掉，
//1)如果没有就把它加入到最大无关向量组中，并把他以及他和此前的硬币的线性组合都筛掉
//2)如果有就不理会
//即就是在完全背包求方案数的过程中，统计那些初始没有方案数的物品
//这样就变成一个完全背包问题了

const int N = 110, M = 25010;
int n;
int v[N];
bool f[M];

int main()
{
    int T = 1;
    cin >> T;
    while (T -- )
    {
        cin >> n;
        for (int i = 1; i <= n; ++ i) cin >> v[i];
        sort(v + 1, v + n + 1);//排序的原因见之前的分析

        //我们只需统计所有物品的体积是否能被其他的线性表出
        //因此背包的体积只需设置为最大的物品体积即可
        //res用来记录最大无关向量组的个数
        int m = v[n], res = 0;
        memset(f, 0, sizeof f);
        f[0] = true;    //状态的初值
        for (int i = 1; i <= n; ++ i)
        {
            //如果当前物品体积被之前的物品组合线性筛掉了，则它是无效的
            if (f[v[i]]) continue;
            //如果没有被筛掉，则把它加入最大无关向量组
            res ++ ;
            //筛掉当前最大无关向量组能线性表示的体积
            for (int j = v[i]; j <= m; ++ j)
            {
                f[j] |= f[j - v[i]];
            }
        }
        //输出最大无关向量组的向量个数
        cout << res << endl;
    }
    return 0;
}

35 评论

Snow_raw 2021-09-27 20:25

彩铅助教%%

一只野生彩色铅笔 2021-09-27 21:24

谢谢支持 w

大伟老师的亲传弟子 2022-08-11 19:23

if (f[v[i]]) continue;上方的注释我觉得应该不是当前武平的体积，而是上一次筛出来的体积。对比这道题的二维写法，这个地方是f[i-1][v[i]]

大伟老师的亲传弟子 2022-08-11 19:23

物品

codingMIKU 2022-09-15 19:12

没毛病啊注释，就是当前物品的体积

walili 2023-01-10 21:54 回复了大伟老师的亲传弟子的评论

捉到了,哈哈哈

大伟老师的亲传弟子 2023-01-11 20:52 回复了 walili 的评论

哈哈哈哈哈，可以的，这么快就刷到提高课了，进步神速

_cabbage_ 2023-04-04 16:26

|=是干什么用的啊？？

相守八十与你 2023-04-06 20:53

就是二者一个为1，则都为1

Equinox_9 11个月前

%%%

Wzzh 2024-01-16 19:39

很清晰！

秧歌star 2023-09-12 21:45

上个学期刚学完线代，愧对老师

acwing_92650 2023-04-15 12:59

orz

青阳 2022-10-03 16:57

线代学的很浅，没想到最大线性无关组

月无阴晴 2022-05-03 14:19

y总的那个性质一为什么成立啊

海问香 2022-05-17 16:59

$ai$ = 0*( $a0$ +… + $a(i - 1)$ ) + $ai$ + 0*( $a(i + 1)$ + … + $am$ )

gtt 2022-04-02 11:06

orz ! ! !

八妹 2022-03-08 21:35

楼主讲的很清楚，连集合划分都出来了，但是把这个题写成二维的好像不行，或者是我本身就写错了，楼主能看一下二维怎么写吗，多谢^^

平凡的人生不平凡的梦 2022-04-21 14:19

我也是，用二维f就是过不了；
for(int i=1;i<=n;i){
for(int j=0;j<=m;j){
f[i][j]=f[i-1][j];
if(j>=a[i])f[i][j]=f[i][j] || f[i][j-a[i]];
}
}
不知道哪里有问题

平凡的人生不平凡的梦 2022-04-21 14:25

懂了，二维你要注意一下if(f[v[i]])continue;
应该写成if(f[i-1][v[i]])continue;而不是if(f[i][v[i]])continue;

大伟老师的亲传弟子 2022-08-11 19:51 回复了平凡的人生不平凡的梦的评论

能看看具体的代码吗？我改了还是不行

齐山风 1个月前回复了大伟老师的亲传弟子的评论

#pragma GCC optimize("Ofast","inline","unroll-loops","no-stack-protector")
#include <bits/stdc++.h>
#define MountainRain main
//#define int long long
//#define double long double
#define INF 0x3f3f3f3f
#define endl '\n'
#define fi first
#define se second
using namespace std;typedef pair<int,int> PII;typedef long long LL;typedef unsigned long long ULL;int in(){int x=0,y=0;char c=0;while(!isdigit(c))y|=c=='-',c=getchar();while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();return y?-x:x;}void out(int x){if(x<0)putchar('-'),x=-x;if(x>9)out(x/10);putchar(x%10+'0');}
const int N=110,M=25010;
int n;
int v[N];
bool f[N][M];
//f[i][j]=f[i-1][j]|f[i][j-v[i]]
void solve()
{
    cin>>n;
    for(int i=1;i<=n;++i)cin>>v[i];
    sort(v+1,v+n+1);
    int m=v[n],res=0;
    memset(f,0,sizeof f);
    f[0][0]=1;
    for(int i=1;i<=n;++i)
    {
        if(!f[i-1][v[i]])res++;
        for(int j=0;j<=m;++j)
        {
            if(j>=v[i])f[i][j]=f[i-1][j]|f[i][j-v[i]];
            else f[i][j]=f[i-1][j];
        }
    }   
    cout<<res<<endl;
}
signed MountainRain()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cout.setf(ios::fixed),cout.precision(2);
    int T=1;cin>>T;
    while(T--)solve();
    return 0;
}

齐山风 1个月前回复了大伟老师的亲传弟子的评论

注意，对于二维的这里是不能continue的！因为你二维在算的时候会用到上一层的状态，你要是直接continue了那这一层就啥都没有了，全是0，就是说，即使他没用，也要利用他把之前的所有状态转移过来。而如果是一维的，他天然的继承了前面的状态，所以continue无所谓。

齐山风 1个月前回复了大伟老师的亲传弟子的评论

所以正确的脑回路应该是先写出来二维版本的，然后在二维的基础上降维。紧接着发现用被筛掉的v[i]来更新v[i]后面的数是不必要的，因为如果后面的数可以用含v[i]的方案表示出来，v[i]又可以被v[i]之前的数表示出来，于是v[i]后面的数一定可以用v[i]之前的数表示出来，也即一定会不需要v[i]就可以被更新，于是再把那个if(!f[v[i]])res++给优化掉。

#pragma GCC optimize("Ofast","inline","unroll-loops","no-stack-protector")
#include <bits/stdc++.h>
#define MountainRain main
//#define int long long
//#define double long double
#define INF 0x3f3f3f3f
#define endl '\n'
#define fi first
#define se second
using namespace std;typedef pair<int,int> PII;typedef long long LL;typedef unsigned long long ULL;int in(){int x=0,y=0;char c=0;while(!isdigit(c))y|=c=='-',c=getchar();while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();return y?-x:x;}void out(int x){if(x<0)putchar('-'),x=-x;if(x>9)out(x/10);putchar(x%10+'0');}
const int N=110,M=25010;
int n;
int v[N];
bool f[M];
//f[i][j]=f[i-1][j]|f[i][j-v[i]]
void solve()
{
    cin>>n;
    for(int i=1;i<=n;++i)cin>>v[i];
    sort(v+1,v+n+1);
    int m=v[n],res=0;
    memset(f,0,sizeof f);
    f[0]=1;
    for(int i=1;i<=n;++i)
    {
        if(!f[v[i]])res++;
        for(int j=v[i];j<=m;++j)
            f[j]=f[j]|f[j-v[i]];
    }
    cout<<res<<endl;
}
signed MountainRain()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cout.setf(ios::fixed),cout.precision(2);
    int T=1;cin>>T;
    while(T--)solve();
    return 0;
}