最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划
题目描述
小明有 $m$ 块钱，现有 $10$ 元， $20$ 元， $50$ 元， $100$ 元 的书
每本书可以购买多次，求小明有多少种买书方案
分析
一共有 $n$ 个物品，每个物品有体积 $v_i$，价值 $w_i$，每个物品能够选多次
求总体积不超过 $m$ 的方案数
这是一道裸的 完全背包问题 求解方案数
废话不多说，直接上 闫氏DP分析法
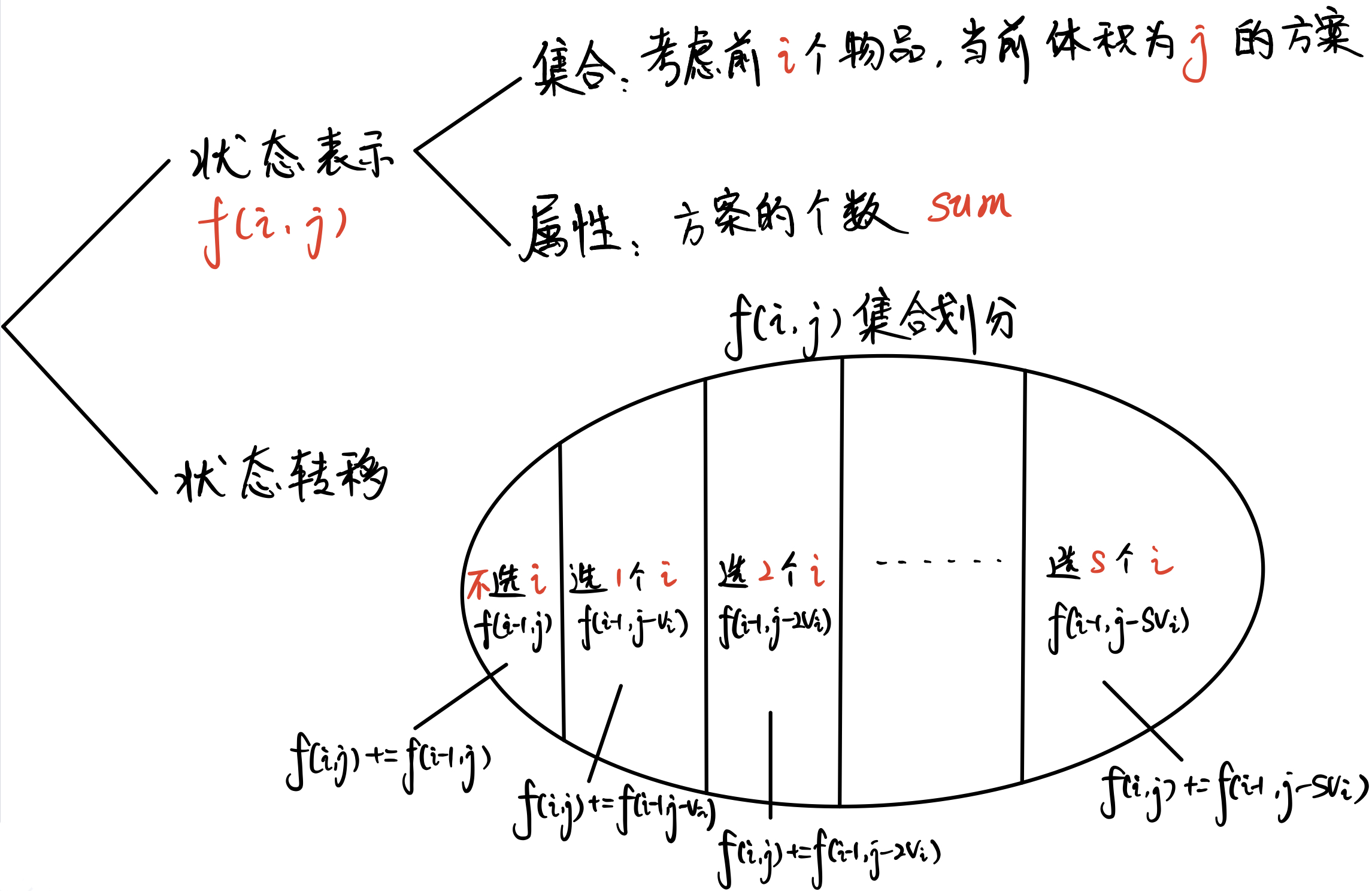
闫氏DP分析法
初始状态：f[0][0]
目标状态：f[n][m]
Code（朴素版）
最坏时间复杂度：$O(n^2\times m)$
#include <iostream>
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = {0, 10, 20, 50, 100};
int f[N][M];
int main()
{
//input
cin >> m;
//dp
f[0][0] = 1;
for (int i = 1; i <= n; ++ i)
{
for (int j = 0; j <= m; ++ j)
{
for (int k = 0; v[i] * k <= j; ++ k)
{
f[i][j] += f[i - 1][j - v[i] * k];
}
}
}
//output
cout << f[n][m] << endl;
return 0;
}
完全背包—经典优化
观察 $f(i,j)$ 的 状态转移方程 进行变形
$$ \begin{matrix} f(i, j) &=& f(i-1,j) &+& f(i-1,j-v_i) &+& \cdots &+& f(i-1,j-sv_i) \\\ f(i, j-v_i) &= &&&f(i-1, j-v_i) &+& \cdots &+& f(i-1,j-sv_i) \end{matrix} $$
由上述两个等式可以获得如下递推式：
$$ f(i,j) = f(i-1,j) + f(i, j-v_i) $$
把这个等式作为 状态转移方程 ，就可以把时间复杂度优化到 $O(n\times m)$
同时，观察到该 转移方程 对于第 i 阶段的状态，只会使用第 i-1 层和第 i 层的状态
因此我们也可以采用 01背包 的 空间优化方案
时间复杂度：$O(n\times m)$
空间复杂度：$O(m)$
#include <iostream>
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = {0, 10, 20, 50, 100};
int f[M];
int main()
{
//input
cin >> m;
//dp
f[0] = 1;
for (int i = 1; i <= n; ++ i)
{
for (int j = v[i]; j <= m; ++ j)
{
f[j] += f[j - v[i]];
}
}
//output
cout << f[m] << endl;
return 0;
}
不是不超过，是体积正好为m的方案数
我也栽在这里了呜呜呜
那个朴素版本，为什么01背包问题中的朴素版本需要将所有物品的f[i][0]都初始化为1，这里只需要初始化f[0][0]且初始其他行的f[i][0]会出错呢反而，不是应该前i件物品放入总重为0的背包中的方案还是只有1嘛
大佬请问解决了吗？我也想问这个问题
我当时写的时候是觉得这条代码：$f[i][j] += f[i - 1][j - v[i] * k];$，如果将首列全部置为1的话，我直接做加等于操作会导致第一列的值越来越大，要不就设置一个限制条件，当j > w[i]的时候做这个操作，小于的时候直接等于，这样我试过也是正确的好像
我觉得一维优化后的令f[0] = 1和二维时的令f[0~n][0] = 1是等价的。一维滚动数组一直把f[0] =1这个值保留下去，也就相当于遍历到任意i的时候都有f[0] = 1，那不就是等价于令f[0~n][0] = 1吗？所以我感到疑惑，觉得这里优化前和优化后的代码是矛盾的。。。
搞明白了吗？我也遇见这个问题了
搞明白了吗？我也遇见这个问题了
不等价，二维的那个 f[1~n][0] 都会加上上一个的 f[(1~n)-1][0] ,因此f[1~n][0]都会是 1 , 相当于是迭代过程中给他初始化了。提前令f[0~n][0] = 1的话反而达不到预设的效果。。。
再想想
我认为是这样的: f[0~n][0] = 1实际上是同一个状态。而你状态转移的时候用的加，如果提前使得f[1~n][0] = 1实际上是重复计算了这一个状态
因为 循环里处理了其他f[i][0]的情况，即f[2][0] += f[1][0]，此时f[2][0]就是1了（相当于初始化）。如果你前面再初始化的话就重复了
请问那个优化的方程最后不是那个方程后面多了一项嘛
不会多的，因为s值是一样的，原因：j这么大的空间中，最多能装下几个vi?当然数量是固定的，设为s，所以两个式子中的s是一样的，最后一项就是一样的。
多重背包会多一项吧，完全背包不会多
这个dp递推式优化好强啊。
因为面值最小的10的，所以其实在第二个循环的时候以10为单位递增可以更快一些(PS:只是因为所有面值都是10的倍数，因此不具有普适性)
为啥
f(i,j − v)比f(i, j)少了一项，根据f(i, j)表示的具体含义，不应该是一样的项数吗假设前一个方程最后是 (i , j-svi ) 这里表示 v[i]最多选 s个，如果多选一个j-(s+1)vi 必然< 0 ，显然超过了总价钱或体积，所以后一个方程比前一个少了第
一项
f(i, j)的含义是前i个物品中选，总体积不超过j，f[i][j] = f[i - 1][j] + f[i - 1][j - v] + ... + f[i - 1][j - sv]，然后f[i][j - v] = f[i - 1][j - v] + f[i - 1][j - 2v] + ... + f[i - 1][j - kv]，而且k = s - 1，推不出来f[i][j] = f[i - 1][j] + f[i][j - v]，不应该是f[i][j] = f[i - 1][j] + f[i][j - v] + f[i - 1][j - sv]吗要如何证明
f[i - 1][j - sv] = 0这个是看的 第 i的物品 最多是 j-sv 第二个方程最后也应该是 j-sv 啊 因为是同一个物品的体积是一样的
f[i][j - v]的含义是第i个物品没错，但是j - v的含义不是体积不超过j - v吗，正式因为同一个物品，所以在相同单位体积下，最终能选的数量自然就少1了啊，所以才会有k = s - 1朴素版本的初始化能否用：n本书，0元钱，对应1种方案？
代码for(int i =0 ; i <= 4; i ++) f[i][0] = 1;
你是f[0][0] = 1;
Orz 好题解
彩铅佬我的超人呜呜呜！
借个图，谢谢大佬 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
这个dp递推式优化好强啊。
这个dp递推式优化好强啊。
这个dp递推式优化好强啊。
大佬您的字迹怎么就这么好看呢？
恰好等于
=，不用f[0]=1,f[i]=0x3f3f3f3f3f吗体积恰好求方案数 ＝1，方案数都不能初始化正无穷
背包这里关于恰好的问题，y总有过详细讲解吗？
小呆呆巨巨写过一篇dp初始化的探究，可以了解一下。
哈哈，能仙人指路一下吗？
https://blog.csdn.net/qq_52765554/article/details/123157907?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166005842816782395365462%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=166005842816782395365462&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-3-123157907-null-null.nonecase&utm_term=%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98&spm=1018.2226.3001.4450
请问为什么f[0] = 1呢
因为当前的状态是由上一个状态转移过来的，f[0]也就是花费为0的选法有多少种，很显然什么都不能选，所以f[0]的选法只有一种，之后的所有状态都是由f[0]转移过来的。
非常感谢~
巨巨 有个问题， 假设n元钱不全部用完，这道题怎么写。。🙄
模型是背包问题最优方案数，要做两次DP，提高课后面有这道题我记得
巨巨 可能理解错了， 上午想了想，如果不把钱用完，那么只需要改变集合的含义和初始化即可。
f[i]表示和<=i的方案数的集合
确实 (𖦹.𖦹) 这题是直接把方案数作为状态属性的，你是对的
小于等于n的所有方案数是不是可以在这个dp的后面求一遍前缀和得出s[n]呢.😢
就相当于原来只能从f1开始转移，现在变成了可以从f1，f2，f3，f4开始转移，感觉类似于二进制，四个数构成了全部的状态