最近在补全提高课所有题目的题解，引荐一下汇总的地方提高课题解汇总

题目描述

给定一个 $n \times m$ 的矩阵，起点位置在 $(1,1)$，终点位置是 $(n, m)$

接着给定该矩阵上，每个位置$(x,y)$上的物品的价值$w$

现需要我们制定一个方案：

从起点出发，只能向右或向下走，如何走到终点，才能使经过的所有格子的物品总价值最大

题解

这题是一道标准的动态规划问题，模型是数字三角形

我们先来分析一下

如果要进行动态规划，则用来表示当前状态的参数有哪些？

1. 当前走到第$i$行
2. 当前走到第$j$列

于是乎，我们可以开二维数组f[i][j]来存储当前在$i$行$j$列的状态

而f[i][j]的值，就是表示从起点走到该点经过的所有格子的价值总和的最大值

则最终答案的状态就是f[n][m]

然后再考虑状态转移方程

因为限制了只能向右或向下走，因此当前状态f[i][j]只能由f[i-1][j]或f[i][j-1]转移过来

闫氏DP分析法

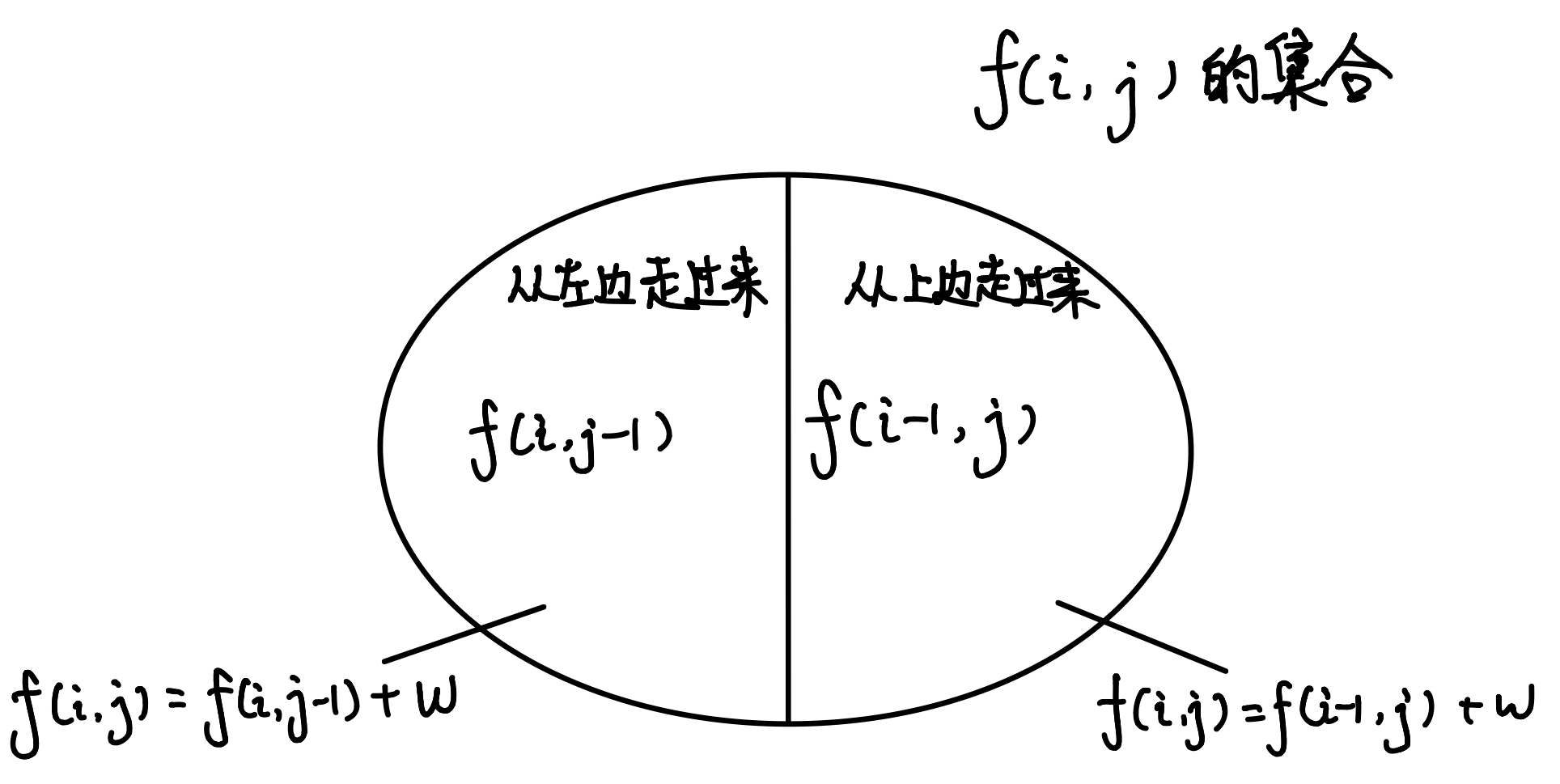
$$ \begin{cases} 状态表示\mathrm{f(i,j)} \begin{cases} 属性: 从起点出发，走到第\mathrm{i}行第\mathrm{j}列的所有方案 \\\ 集合: 方案中的路线经过的所有物品的总价值最大 Max \end{cases} \\\ 状态转移 f(i,j) = max\{f(i - 1, j), f(i, j - 1)\} + w(i,j) \end{cases} $$

集合划分

Code(循环写法)

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int T;
int n, m;
int w[N][N];
int f[N][N];

int main()
{
    cin >> T;
    while (T -- )
    {
        memset(w, 0, sizeof w);
        memset(f, 0, sizeof f);
        cin >> n >> m;

        for (int i = 1; i <= n; ++ i)
        {
            for (int j = 1; j <= m; ++ j)
            {
                cin >> w[i][j];
            }
        }

        //dp
        for (int i = 1; i <= n; ++ i)
        {
            for (int j = 1; j <= m; ++ j)
            {
                f[i][j] = max(f[i][j - 1], f[i - 1][j]) + w[i][j];
            }
        }

        cout << f[n][m] << endl;
    }
    return 0;
}

Code(记忆化搜索写法)

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;

int T;
int n, m;
int w[N][N];
int f[N][N];

int dp(int x, int y)
{
    if (f[x][y] >= 0) return f[x][y];
    if (x < 1 || x > n || y < 1 || y > m) return f[x][y] = -INF;
    if (x == 1 && y == 1) return f[x][y] = w[x][y];

    int t = 0;
    t = max(t, dp(x - 1, y) + w[x][y]);
    t = max(t, dp(x, y - 1) + w[x][y]);
    return f[x][y] = t;
}
int main()
{
    cin >> T;
    while (T -- )
    {
        memset(w, 0, sizeof w);
        memset(f, -1, sizeof f);
        cin >> n >> m;

        for (int i = 1; i <= n; ++ i)
        {
            for (int j = 1; j <= m; ++ j)
            {
                cin >> w[i][j];
            }
        }
        cout << dp(n, m) << endl;
    }
    return 0;
}