题目分析

数位$dp$

首先考虑状态表示
$dp(i , j , k)$ 表示 前$i$个字符中，更改字符数为$j$的，结尾状态为$k$的方案数

题目要求不含110子串，所以考虑下状态$k$的种类

以0结尾 ，00和10 都一样，后面可以添加任意0或1
以01结尾 ，后面可以添加任意0或1
以11结尾 ，后面只能添加1

状态转移图如下

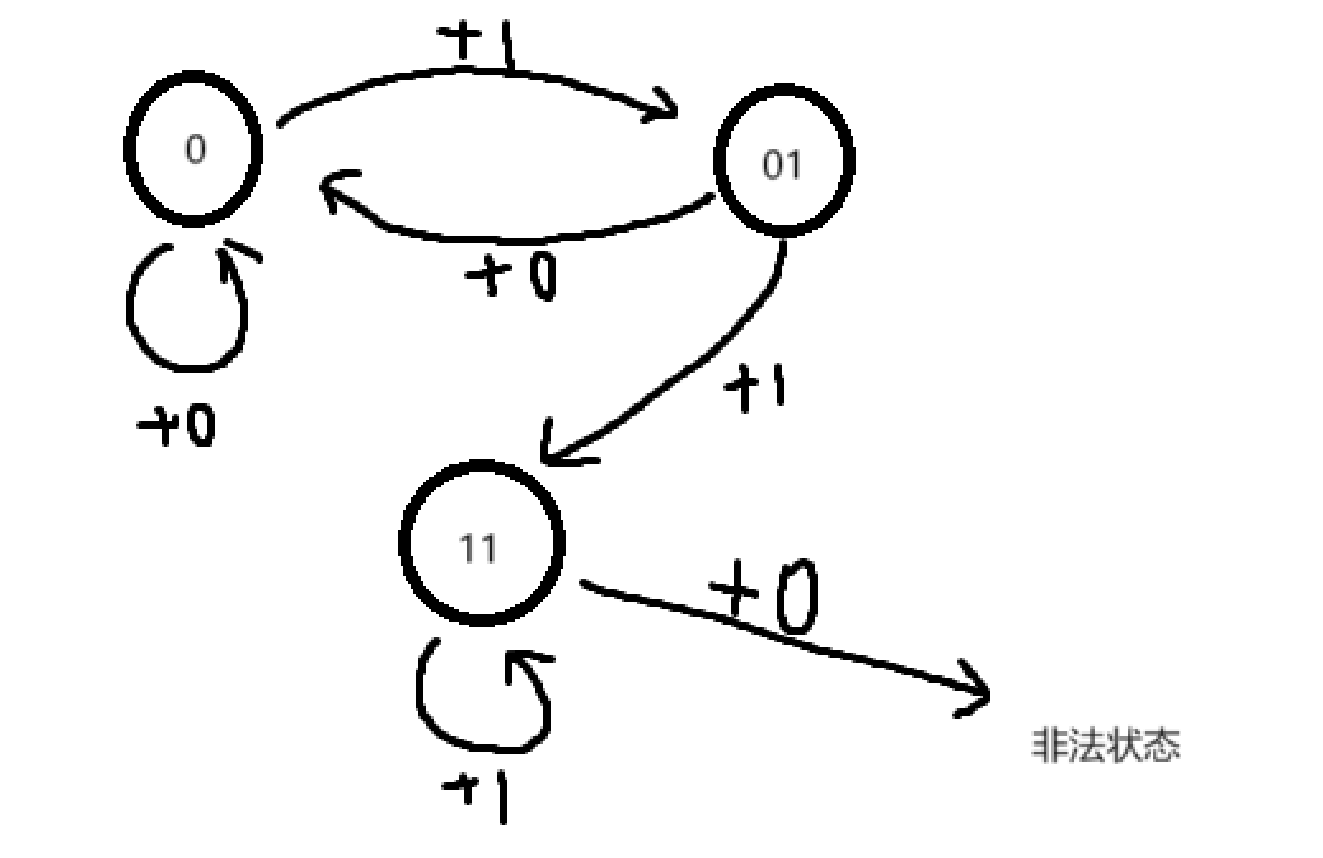
那么如果当前字符为$x$，那么有两种转移方式，一种是直接在结尾添加$x$，不消耗$j$的次数。
还可以添加$x ⊕ 1$，同时消耗$j$次数。

最后答案就是所有不超过修改次数$k$的总方案数

代码 $MLE$

#include<bits/stdc++.h> 
#define int long long
using namespace std;
const int N = 5001 , MOD = 998244353;

int dp[N][N][3]; // 0表示以0结尾 1表示以一个1结尾 2表示以两个1结尾
int n , k ;
char s[N];
signed main( )
{
    cin >> n >> k >> s + 1;
    dp[0][0][0] =  1;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 0 ; j <= k ; j ++)
            if(s[i] == '1')
            {
                if(j >= 1) dp[i][j][0] = (dp[i][j][0] + dp[i - 1][j - 1][0] + dp[i - 1][j - 1][1]) % MOD;
                dp[i][j][1] = (dp[i][j][1] + dp[i - 1][j][0]) % MOD;
                dp[i][j][2] = (dp[i][j][2] + dp[i - 1][j][1] + dp[i - 1][j][2]) % MOD;
            }
            else 
            {
                dp[i][j][0] = (dp[i][j][0] + dp[i - 1][j][0] + dp[i - 1][j][1]) % MOD;
                if(j >= 1)dp[i][j][1] = (dp[i][j][1] + dp[i - 1][j - 1][0]) % MOD;
                if(j >= 1) dp[i][j][2] = (dp[i][j][2] + dp[i - 1][j - 1][1] + dp[i - 1][j - 1][2]) % MOD;
            }

    int res = 0;
    for(int i = 0 ; i <= k ; i ++)
        res = (res + dp[n][i][0] + dp[n][i][1] + dp[n][i][2]) % MOD;

    cout << res << '\n';

    return 0;
}

内存超了，所以要用到滚动数组

#include<bits/stdc++.h> 
#define int long long
using namespace std;
const int N = 5001 , MOD = 998244353;

int dp[2][N][3]; // 0表示以0结尾 1表示以一个1结尾 2表示以两个1结尾
int n , k ;
char s[N];
signed main( )
{
    cin >> n >> k >> s + 1;
    dp[0][0][0] = 1;
    for(int i = 1 ; i <= n ; i ++)
    {
        int l = i % 2;
        for(int j = 0 ; j <= k ; j ++)
            if(s[i] == '1')
            {
                if(j >= 1) dp[l][j][0] = (dp[l][j][0] + dp[l ^ 1][j - 1][0] + dp[l ^ 1][j - 1][1]) % MOD;
                dp[l][j][1] = (dp[l][j][1] + dp[l ^ 1][j][0]) % MOD;
                dp[l][j][2] = (dp[l][j][2] + dp[l ^ 1][j][1] + dp[l ^ 1][j][2]) % MOD;
            }
            else 
            {
                dp[l][j][0] = (dp[l][j][0] + dp[l ^ 1][j][0] + dp[l ^ 1][j][1]) % MOD;
                if(j >= 1) dp[l][j][1] = (dp[l][j][1] + dp[l ^ 1][j - 1][0]) % MOD;
                if(j >= 1) dp[l][j][2] = (dp[l][j][2] + dp[l ^ 1][j - 1][1] + dp[l ^ 1][j - 1][2]) % MOD;
            }
        memset(dp[l ^ 1] , 0 , sizeof(dp[l ^ 1]));
    }


    int res = 0;
    for(int i = 0 ; i <= k ; i ++)
        res = (res + dp[(n % 2)][i][0] + dp[(n % 2)][i][1] + dp[(n % 2)][i][2]) % MOD;

    cout << res << '\n';

    return 0;
}