快速幂可以快速的求出来a^k%p的结果在O(logk)时间内
反复平方法
预处理出来下面这些值,用这些值来组合出来a^k

把k拆分成logk个数的和,把k换成二进制表示
如何预处理出来logk个数
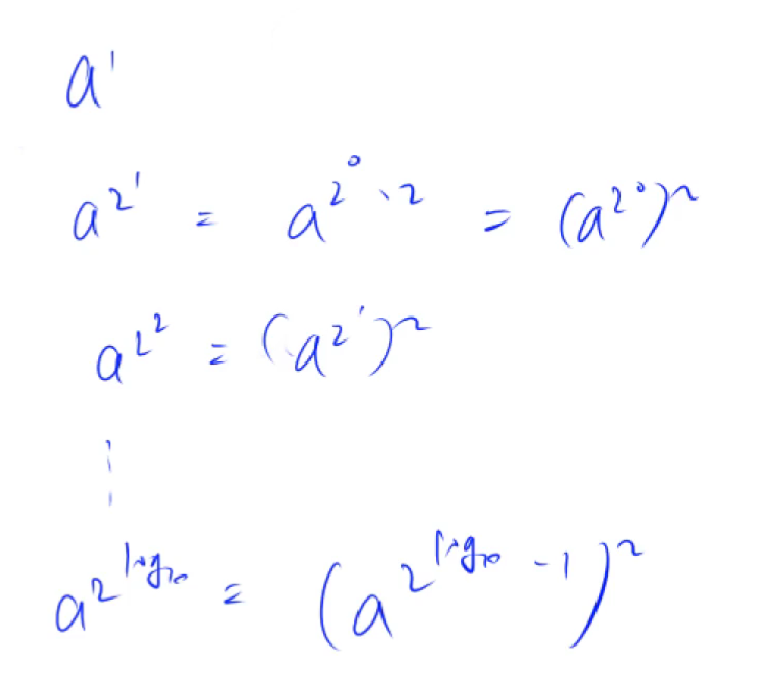
例子
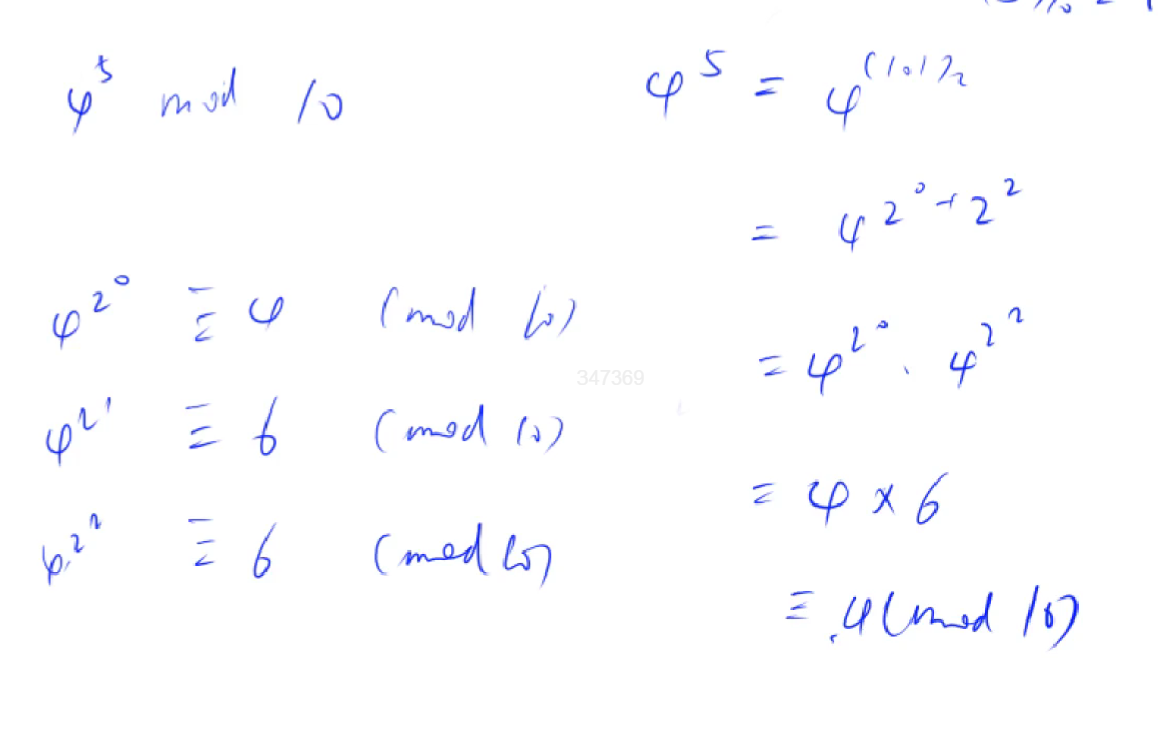
就是将a^k的k用二进制表示出来,2^0+2^1+…2^m=k,将a^k转化为求a^2^0*a^2^1…
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;//两个10^9相乘会爆int,数论很多题都会用到LL
//返回a^k%p的结果
int n;
int qmi(int a,int k,int p)
{
int res=1;//答案,最开始存的是a^0
//本质上是求k的二进制表示
while(k)
{
if(k&1)//如果k的末位是1的话 为什么见收藏题解
res=(LL)res*a%p;//将res临时转换为long long 型做运算,不是永久转换 %p不能省
//把k的末位删掉
k>>=1;
//变成a^2
a=(LL)a*a%p;//不能省
}
return res;
}
int main()
{
scanf("%d",&n);
while(n--)
{
int a,k,p;
scanf("%d%d%d",&a,&k,&p);
printf("%d\n",qmi(a,k,p));
}
return 0;
}

