Codeforces Round 924 (Div. 2)[A-D]

进算竞小群加我

A. Rectangle Cutting

Bob 有一个大小为 $a \times b$ 的矩形。他试图通过平行于原始矩形的一条边进行切割，将该矩形切割成两个边长为整数的矩形。然后鲍勃尝试从两个生成的矩形中形成一些其他矩形，并且他可以根据自己的意愿旋转和移动这两个矩形。

请注意，如果两个矩形仅相差 $90^{\circ}$ 旋转，则它们被视为相同。例如，矩形 $6 \times 4$ 和 $4 \times 6$ 被认为是相同的。

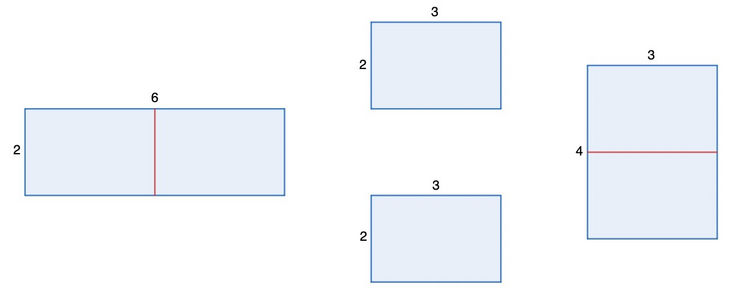
这样，由 $2 \times 6$ 矩形可以组成另一个矩形，因为它可以被切割成两个 $2 \times 3$ 矩形，然后用这两个矩形可以组成 $4 \times 3$ 矩形，这与 $2 \times 6$ 矩形不同} 长方形。

然而，从 $2 \times 1$ 矩形不能形成另一个矩形，因为它只能被切割成两个 $1 \times 1$ 矩形，并且由此只能形成 $1 \times 2$ 和 $2 \times 1$ 矩形，这被认为是相同。

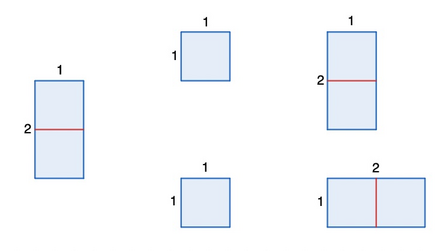
帮助鲍勃确定他是否可以获得其他矩形，或者他是否只是在浪费时间。

枚举所有的可能,看一下方案数

https://codeforces.com/contest/1928/submission/245800061

// Codeforces - Codeforces Round 924 (Div. 2) A. Rectangle Cutting
// https://codeforces.com/contest/1928/problem/0 2024-02-11 17:36:03

#include <bits/stdc++.h>
using namespace std;
#define all(a) begin(a), end(a)
#define int long long
int n, m;
using pii = pair<int, int>;
template <class T, class U>
ostream &operator<<(ostream &os, const std::pair<T, U> &p) {
  os << "" << p.first << " " << p.second << endl;
  return os;
}
void solve() {
  cin >> n >> m;
  set<pii> S;
  if (n > m) swap(n, m);
  S.emplace(n, m);
  if (n % 2 == 0 or m % 2 == 0) {
    if (n % 2 == 0) {
      S.emplace(min(n / 2, 2 * m), max(n / 2, 2 * m));
    }
    if (m % 2 == 0) {
      S.emplace(min(m / 2, 2 * n), max(m / 2, 2 * n));
    }
    if (S.size() >= 2)
      cout << "Yes\n";
    else
      cout << "No\n";
  } else
    cout << "No\n";
}

signed main() {
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);
  int __;
  cin >> __;
  while (__--) solve();
  return 0;
}

B. Equalize

Vasya 有两个爱好 - 向数组添加排列 $^{\dagger}$ 和查找最常出现的元素。最近，他发现了一个数组 $a$ ，并决定在对数组 $a$ 添加一些排列后，找出与数组 $a$ 中相同数量的元素的最大数量。

更正式地说，Vasya 必须恰好选择一种长度为 $n$ 的排列 $p_1, p_2, p_3, \ldots, p_n$ ，然后根据规则 $a_i := a_i + p_i$ 更改数组 $a$ 的元素。之后，Vasya 计算每个数字在数组 $a$ 中出现的次数，并取这些值中的最大值。你需要确定他可以获得的最大值。

$^{\dagger}$ 长度为 $n$ 的排列是由 $n$ 个从 $1$ 到 $n$ 的不同整数以任意顺序组成的数组。例如， $[2,3,1,5,4]$ 是排列，但 $[1,2,2]$ 不是排列（ $2$ 在数组中出现两次）， $[1,3,4]$ 也不是排列（ $n=3$ 但数组中有 $4$ ）大批）。

每个测试由多个测试用例组成。第一行包含一个整数 $t$ ( $1 \leq t \leq 2 \cdot 10^4$ ) - 测试用例的数量。然后是测试用例的描述。

每个测试用例的第一行包含一个整数 $n$ ( $1 \le n \le 2 \cdot 10^5$ ) - 数组 $a$ 的长度。

每个测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$ ( $1 \le a_i \le 10^9$ ) — 数组 $a$ 的元素。

保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$ 。

滑动窗口

https://codeforces.com/contest/1928/submission/245810883

// Codeforces - Codeforces Round 924 (Div. 2) B. Equalize
// https://codeforces.com/contest/1928/problem/B 2024-02-11 17:38:48

#include <bits/stdc++.h>
using namespace std;
#define all(a) begin(a), end(a)
#define int long long
int n, m;
void solve() {
  map<int, int> mp;
  cin >> n;
  int _n = n;
  set<int> S;
  vector<int> a(n);
  for (int i = 0; i < n; i++) cin >> a[i], S.emplace(a[i]);
  sort(all(a));
  vector<int> _a;
  n = S.size();
  for (auto i : S) _a.emplace_back(i);
  int ans = 0;
  for (int i = 0; i < n; i++) {
    ans = max(ans, upper_bound(all(_a), _a[i] + _n - 1) - (begin(_a) + i));
  }
  cout << ans << "\n";
}

signed main() {
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);
  int __;
  cin >> __;
  while (__--) solve();
  return 0;
}

C. Physical Education Lesson

在一所著名的学校里，有一节体育课。像往常一样，每个人都排成一排，并被要求站在 “第 $k$ 个 “的位置上。

众所周知，在 “第一个- $k$ /-第三个 “位置落座的情况如下：第一个 $k$ 人的号码是 $1, 2, 3, \ldots, k$ ，接下来的 $k - 2$ 人的号码是 $k - 1, k - 2, \ldots, 2$ ，接下来的 $k$ 人的号码是 $1, 2, 3, \ldots, k$ ，以此类推。这样，每隔 $2k - 2$ 个位置就重复一次结算。结算示例见 “注释 “部分。

男孩瓦夏经常忘记所有事情。例如，他忘记了上面描述的数字 $k$ 。但是他记得他在队伍中的位置，以及他在结算时得到的数字。请帮助瓦夏理解在给定的限制条件下，有多少个自然数 $k$ 符合要求。

请注意，当且仅当 $k > 1$ 存在时，结算才存在。特别是，这意味着 $k = 1$ 不存在结算。

每个测试由多个测试用例组成。第一行包含一个整数 $t$ ( $1 \leq t \leq 100$ ) — 测试用例的数量。接下来是测试用例的描述。

每个测试用例的唯一行包含两个整数 $n$ 和 $x$ ( $1 \le x < n \le 10^9$ ) - Vasya 在该行中的位置以及 Vasya 在结算过程中收到的数字。

分为两种情况

1. 上坡

$n-x$ 代表着 $z(2k-2)$

$k\ge x$

$n-x=z(2k-2)$

$x=n-z(2k-2)$

$n-z(2k-2)\le k $

$z$ 是 $n-x$ 的因子

可以 $O(\sqrt {n-x})$ 时间内枚举完成

枚举$z∈(n-x)_{因子}$

满足

$x=n-z(2k-2)$

$2k-2=\frac {n-x} z$

$k=\frac {\frac {n-x} z +2} 2$

$k=\frac {n-x} {2z} +1$

$n-z(2k-2)\le k $

1. 下坡

$n+x-2$代表着 $z(2k-2)$

$k \ge x$

$n+x-2=z(2k-2)$

枚举$z∈{(n+x-2)}_{因子}$

可以$O(\sqrt {n+x-2})$ 枚举 $z$

$2k-2=\frac {n+x-2} z$

$k=\frac {n+x-2} {2z} +1$

$k \ge x$

code

Submission #245962526 - Codeforces

// Codeforces - Codeforces Round 924 (Div. 2) C. Physical Education Lesson
// https://codeforces.com/contest/1928/problem/C 2024-02-12 16:45:22

#include <bits/stdc++.h>
using namespace std;
#define all(a) begin(a), end(a)
#define int long long
int n, x;
vector<int> divide2(int x) {
  vector<int> ans;
  for (int i = 2; i <= x / i; i++)
    if (x % i == 0) {
      ans.push_back(i);
      if (i * i != x) ans.push_back(x / i);
    }
  if (x > 1) ans.push_back(x);
  return ans;
}
void solve() {
  cin >> n >> x;
  auto it = divide2(n - x);
  it.emplace_back(1);
  set<int> S;
  for (auto z : it) {
    if ((n - x) % (z * 2) == 0) {
      int k = (n - x) / z / 2 + 1;
      if (k >= x and k >= 2) S.emplace(k);
    }
  }
  auto it2 = divide2(n + x - 2);
  it2.emplace_back(1);
  for (auto z : it2) {
    if ((n + x - 2) % (2 * z) == 0) {
      int k = (n + x - 2) / z / 2 + 1;
      if (k >= x and k >= 2) S.emplace(k);
    }
  }
  cout << S.size() << "\n";
}

signed main() {
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);
  int __;
  cin >> __;
  while (__--) solve();
  return 0;
}

D. Lonely Mountain Dungeons [三分]

曾经，中土世界的人民、精灵、矮人和其他居民聚集在一起，想要夺回被史矛革偷走的宝藏。以这个伟大目标的名义，他们团结在强大的精灵蒂莫西周围，开始策划推翻孤山的统治者。

中土居民的军队将由几个小队组成。众所周知，每对处于不同小队的同一种族的生物，都会为军队的总兵力增加 $b$ 个单位。但由于蒂莫西很难领导一支由大量小队组成的军队，因此由 $k$ 个小队组成的军队的总兵力会减少 $(k - 1) \cdot x$ 个单位。请注意，军队始终由至少一个小队组成。

已知中土世界有 $n$ 个种族，第 $i$ 个种族的生物数量等于 $c_i$ 。帮助中土世界的居民确定他们可以组建的军队的最大兵力。

输入

每个测试由多个测试用例组成。第一行包含一个整数 $t$ ( $1 \le t \le 2 \cdot 10^4$ ) — 测试用例的数量。测试用例的描述如下。

每个测试用例的第一行包含三个整数 $n$ 、 $b$ 和 $x$ ( $1 \le n \le 2 \cdot 10^5$ 、 $1 \le b \le 10^6, 0 \le x \le 10^9$ ) — 比赛数量以及上述常量 $b$ 和 $x$ 。

每个测试用例的第二行包含 $n$ 个整数 $c _ 1, c _ 2, \ldots, c _n$ ( $1 \le c _ i \le 2 \cdot 10^5$ ) — 每个 $n$ 种族的生物数量。

确保所有测试用例的值 $c _ 1 + c _ 2 + \ldots + c _ n$ 之和不超过 $2 \cdot 10^5$ 。

Expand

通过观察题意可以了解

当队列数确定了,那么 所有的分配都是 确定 的

所以 存在 一个最优的 队列数 $x$

我们设 $x$ 为最优的 答案

有个单调性

观察 答案与 变量的 关系可以发现是一个凸函数

所以我们可以在函数上跑一个三分

剩下一个稍微难点的地方就是求组合数了

正难则反,所以我们 求出所有的 组合数

再减去不能组合的配对

那么就是每一队列中的不能配对

然后就很好做了

code

Submission #245968550 - Codeforces

// Codeforces - Codeforces Round 924 (Div. 2) D. Lonely Mountain Dungeons
// https://codeforces.com/contest/1928/problem/D 2024-02-12 17:22:54

#include <bits/stdc++.h>
using namespace std;
#define all(a) begin(a), end(a)
#define int long long
int n, b, x;
template <typename... Args>
void debug(Args &&...args) {
  ((cerr << args << " "), ...), cerr << "\n";
}
void solve() {
  cin >> n >> b >> x;
  int ans = LLONG_MIN;
  vector<int> c(n);
  for (auto &i : c) cin >> i;
  int l = 1LL, r = 2E5 + 1LL;
  auto check = [&](int k) -> int {
    int res = 0LL;
    for (auto it : c) {
      if (it <= k) {
        res += (it) * (it - 1LL) / 2LL;
      } else {
        int avg = it / k;
        int mod = it % k;
        res -= mod * (1LL + avg) * (avg) / 2LL;
        res -= (k - mod) * (avg) * (avg - 1LL) / 2LL;
        res += (it) * (it - 1LL) / 2LL;
      }
    }
    res *= b;
    res -= (k - 1LL) * x;
    return res;
  };
  while (l < r) {
    int lmid = l + (r - l) / 3LL;
    int rmid = r - (r - l) / 3LL;
    if (check(lmid) <= check(rmid))
      l = lmid + 1;
    else
      r = rmid - 1;
  }
  cout << max(check(l), check(r)) << "\n";
}

signed main() {
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);
  int __;
  cin >> __;
  while (__--) solve();
  return 0;
}