算法课要求做多边形游戏，在acwing的OJ上认真水了一下

典型区间DP，首先来DP分析一下

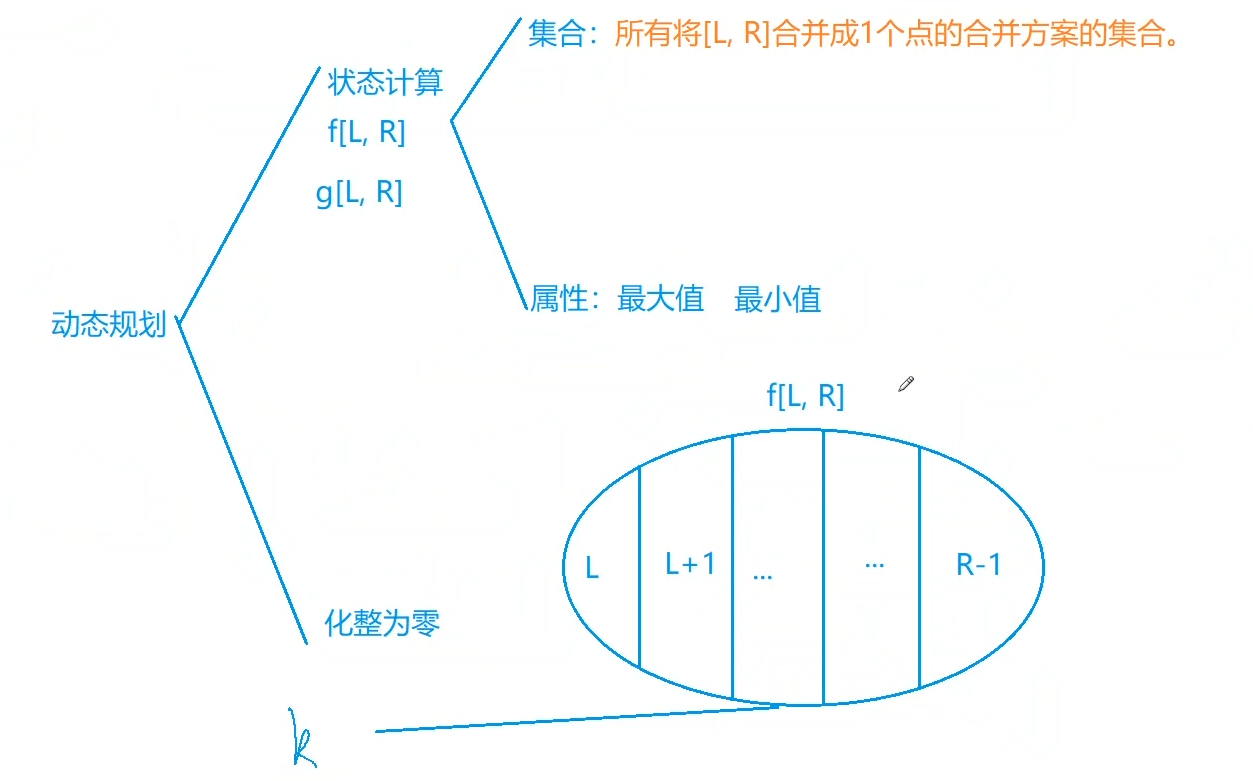
已知i为区间左端点，j为区间右端点

对于加法：

和矩阵相乘一样，直接切分加起来即可
$ f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]) $
$ g[i][j] = min(g[i)[j], g[i][k] + g[k + 1][j]) $

对于乘法

这里要讨论四种情况
$ x1 = g[i][k] * g[k + 1][j] $ 左区间最小值乘右区间最小值
$ x2 = g[i][j] * f[k + 1][j] $ 左区间最小值乘右区间最大值
$ x3 = f[i][k] * g[k + 1][j] $ 左区间最大值乘右区间最小值
$ x4 = f[i][k] * f[k + 1][j] $ 左区间最大值乘右区间最大值
$ f[i][j] = max(f[i][j], max(x1, x2, x3, x4)) $
$ g[i][j] = min(f[i][j], min(x1, x2, x3, x4)) $

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110, INF = 32768;
int n;//n边形
char c[N];//符号
int w[N];//顶点上的整数
int f[N][N], g[N][N];//存储max和min的集合
//f[i][j]为从区间[i,j]中所能合并取得的最高分
//g[i][j]为从区间[i,j]中所能合并取得的最低分
int main(){
    cin >> n;// n边形
    for(int i = 1; i <= n; i ++){
        cin >> c[i] >> w[i];//符号和顶点上的整数
        c[i + n] = c[i];//破环为链，确保每个点对（包括首尾）都能考虑到
        w[i + n] = w[i];
    }
    for(int len = 1; len <= n; len ++){//遍历区间长度
        for(int i = 1; i + len - 1 <= n * 2; i ++){//遍历左端点
            int j = i + len - 1;//得出右端点
            if(len == 1){//区间长度为1时
                f[i][j] = g[i][j] = w[i];//最大最小值就是这个数本身
            }else{//区间长度为2以上时
                f[i][j] = -INF, g[i][j] = INF;//初始化最大最小值
                for(int k = i; k < j; k ++){//开始切分
                    char op = c[k + 1];//取符号
                    int minI = g[i][k], maxI = f[i][k], minJ = g[k + 1][j], maxJ = f[k + 1][j];
                    if(op == 't'){//t代表加号
                        f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]);//maxI + maxJ
                        g[i][j] = min(g[i][j], g[i][k] + g[k + 1][j]);//minI + minJ
                    }else{//乘号
                    int x1 = minI * minJ, x2 = minI * maxJ, x3 = maxI * minJ, x4 = maxI * maxJ;
                        f[i][j] = max(f[i][j], max(max(x1, x2), max(x3, x4)));//x1~x4中取最大，进行更新
                        g[i][j] = min(g[i][j], min(min(x1, x2), min(x3, x4)));//x1~x4中取最小，进行更新
                    }
                }
            }
        }
    }
    int ans = -INF;
    for(int i = 1; i <= n; i ++) ans = max(ans, f[i][i + n - 1]);
    cout << ans << endl; //求出最高分数
    for(int i = 1; i <= n; i ++){
        if(ans == f[i][i + n - 1]){//求出最佳方案
            cout << i << ' ';
        }
    }
    return 0;
}