SPFA算法模板题题解&学习笔记

1 学习笔记

1.1 算法介绍

SPFA是一种单源最短路算法，可以用来算带负环的最短路，是bellman_ford算法的优化

1.2 算法流程

SPFA是用了广搜进行优化，有点类似深搜里的剪枝（个人认为）

我们首先需要一个数组dist，保存每个点的最小点权。

然后用类似广搜的方法，开始遍历图：

while(!q.empty())
{
    int f=q.front();
    q.pop();
    int tt=v[f].size();//我用的是邻接表
    for(int i=0;i<tt;i++)
    {
        ...
    }
}

然后像bellman_ford算法里面，遇到最小值就更新

for(int i=0;i<tt;i++)
{
    int tmp=v[f][i];
    if(dist[tmp]>dist[f]+w[f][i])
    {
        dist[tmp]=dist[f]+w[f][i];//w数组是用来表示边权的
    }
}

然后，像 有边数限制的最短路 题目中的 题解里一样，因为预防出现题目中直接更新到n的办法，需要打标记。与bellman_ford算法不同的是，他只需要将已经放入队列的点标上标记就好了，这样只要不是开始更新当前点的相邻点，其他的点就自然不会更新此数，这也是广搜特性的体现——层次遍历，如图：

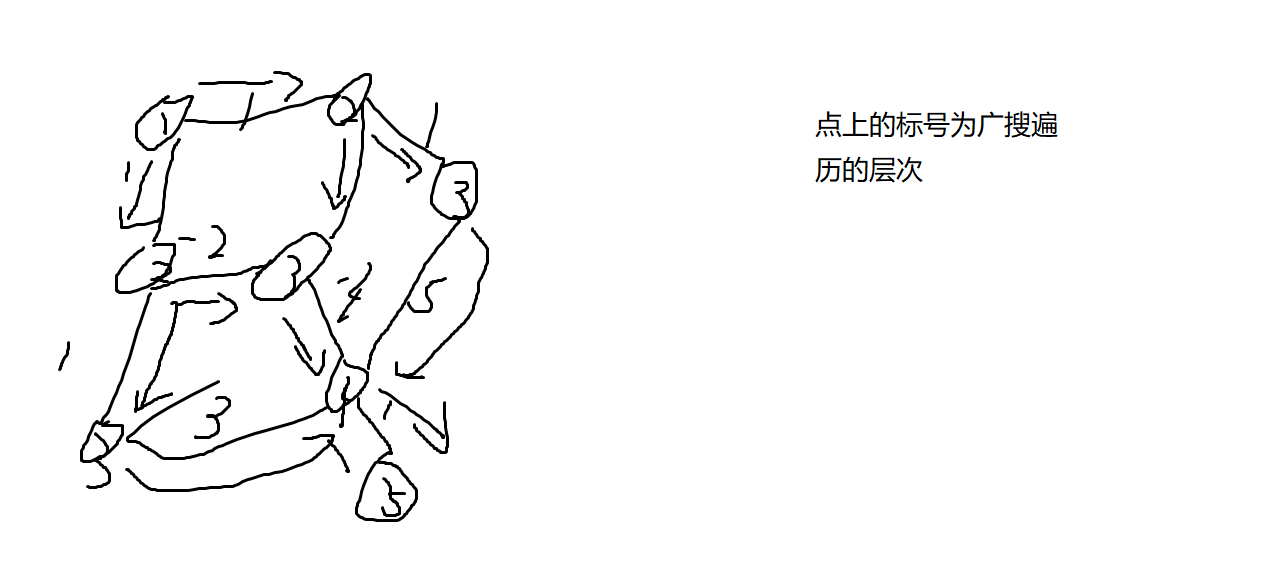
所以核心代码如下：

while(!q.empty())
{
    int f=q.front();
    q.pop();
    st[f]=false;//已经轮到当前节点遍历了，所以可以撤销
    int tt=v[f].size();//我用的是邻接表
    for(int i=0;i<tt;i++)
    {
        int tmp=v[f][i];
        if(dist[tmp]>dist[f]+w[f][i])
        {
            dist[tmp]=dist[f]+w[f][i];//w数组是用来表示边权的
            if(!st[tmp])
            {
                q.push(tmp);
                st[tmp]=true;//打上标记
            }
        }
    }

模板题题解

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
vector<int> v[N],w[N];
int dist[N];
int n,m;
bool st[N];
int spfa()
{
    queue<int> q;
    q.push(1);
    st[1]=true;
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    while(!q.empty())
    {
        int f=q.front();
        q.pop();
        st[f]=false;
        int tt=v[f].size();
        for(int i=0;i<tt;i++)
        {
            int tmp=v[f][i];
            if(dist[tmp]>dist[f]+w[f][i])
            {
                dist[tmp]=dist[f]+w[f][i];
                if(!st[tmp])
                {
                    q.push(tmp);
                    st[tmp]=true;
                }

            }
        }
    }
    return dist[n];
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i=0;i<m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        v[x].push_back(y);
        w[x].push_back(z);
    }
    int t=spfa();
    if(t==0x3f3f3f3f) puts("impossible");//不能使用-1，因为万一答案就是-1，那就GG了
    else printf("%d",t);
}

希望大家喜欢，同时有什么说的不对的欢迎指出来