题目描述

输入一个整数 n ，求斐波那契数列的第 n 项。

假定从 0 开始，第 0 项为 0。

数据范围

0≤n≤39

样例

输入整数 n=5 

返回 5

解法1

暴力递归【自顶向下】

涉及到递归问题画一个递归树，有助于分析算法的复杂度以及寻找算法低效的原因。

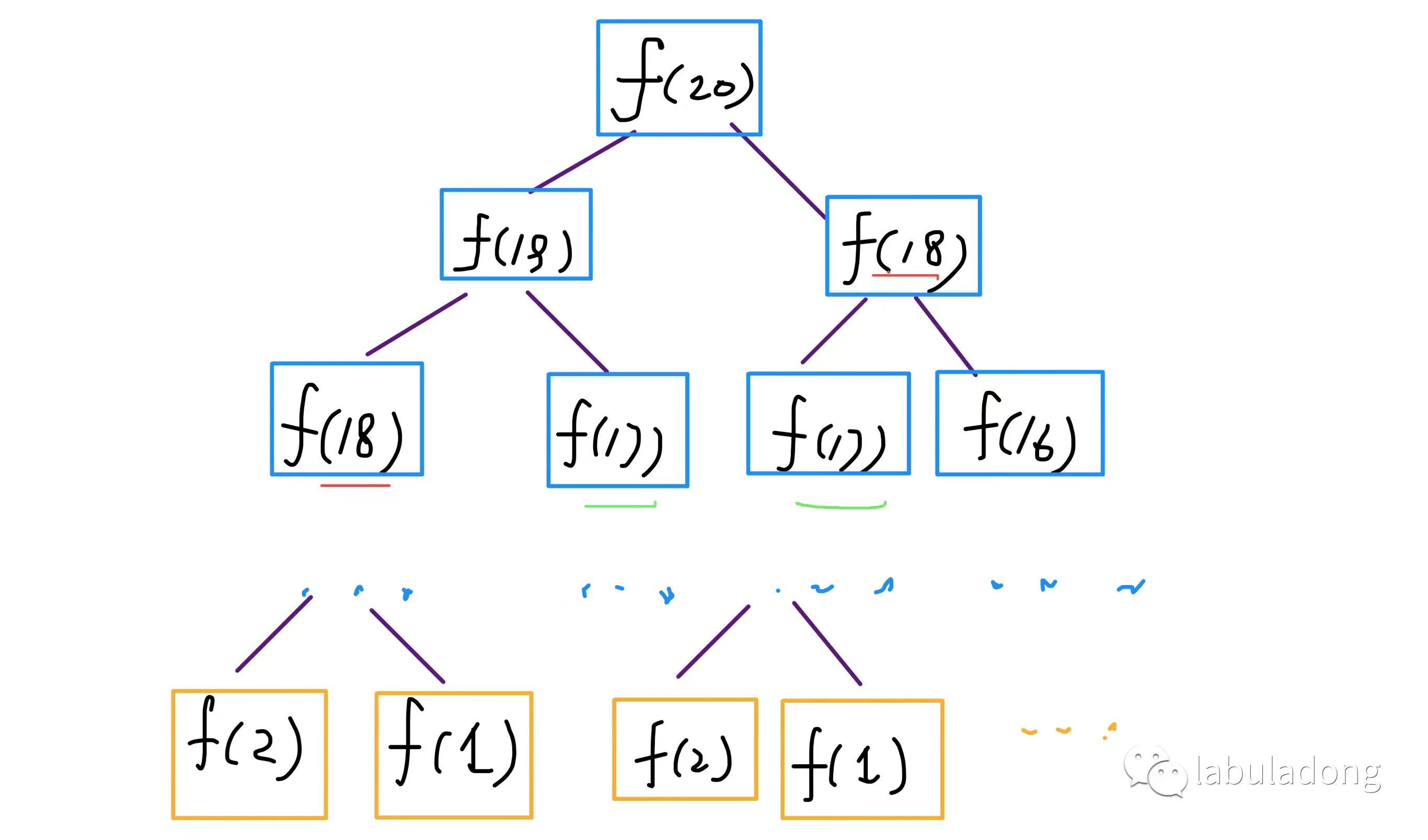
递归算法的时间复杂度=子问题个数×解决一个子问题需要的时间
子问题个数：O(2^n)
解决一个子问题的时间：Fibonacci(n-1)+Fibonacci(n-2) ， 是O(1)
所以时间复杂度是：O(2^n)，爆炸
观察递归树，发现算法低效的原因：存在大量重复计算，即重叠子问题。(重叠子问题是动态规划问题的一个性质)

时间复杂度

$O(2^n)$

参考文献

labuladong

C++代码

class Solution {
public:
    int Fibonacci(int n) {
        if(n==0)  return 0;  //递归结束条件
        if(n==1)  return 1;

        return Fibonacci(n-1)+Fibonacci(n-2);  //递归核心式子
    }
};

解法2

带备忘录的递归 【带记忆的自顶向下】

递归树：

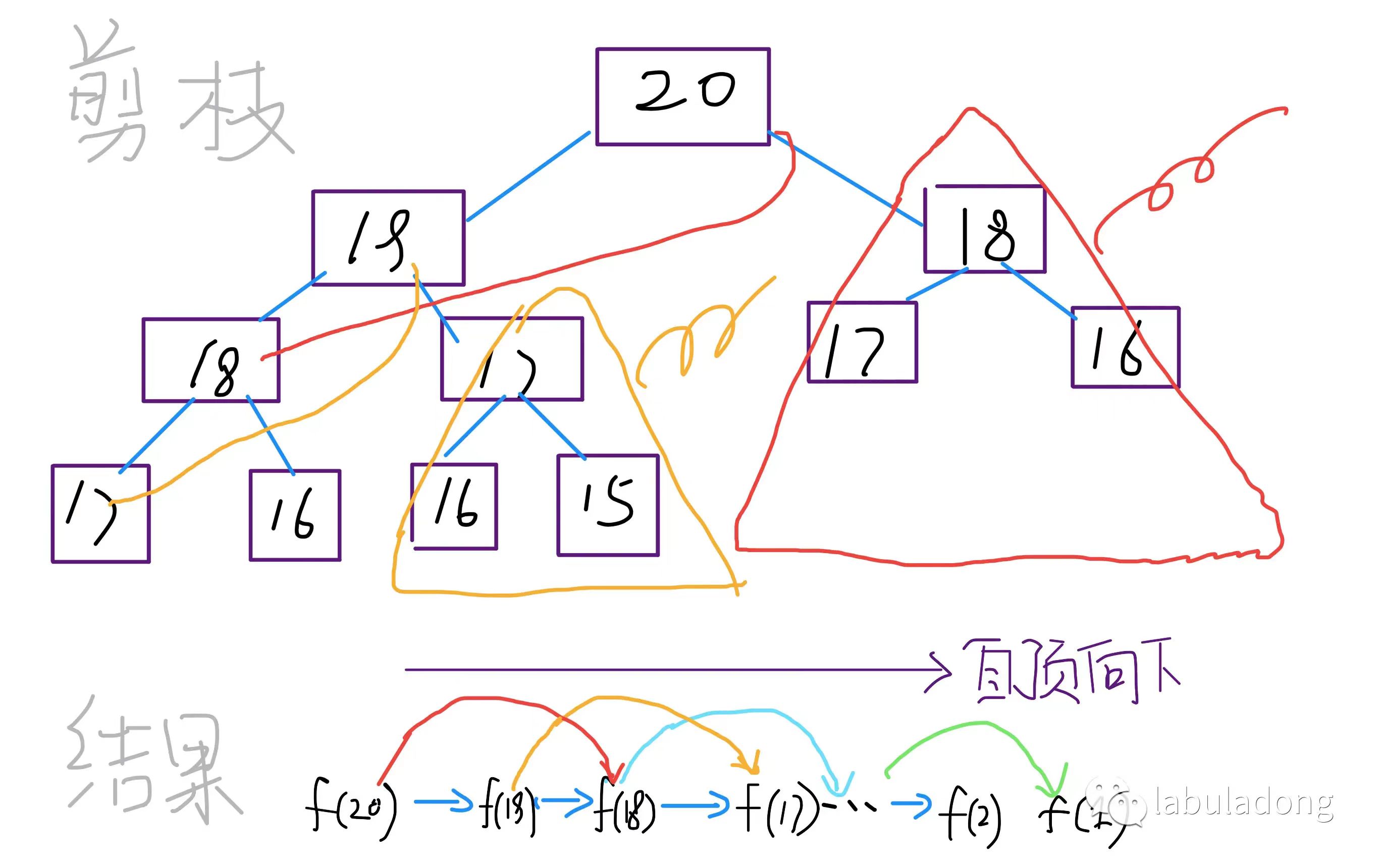
子问题个数：O(n)
解决一个子问题的时间：依旧没有循环，O(1)
所以时间复杂度：$O(n)$

时间复杂度

$O(n)$

参考文献

labuladong

C++ 代码

int memo[42];
class Solution {
public:
    //自带的函数（没办法删，但是可以调用我自己的函数）
    int Fibonacci(int n) {
        memo[0]=0,memo[1]=1;
        my_Fb(n);
    }

    //我写的函数（可以作为最终return结果的函数）
    int my_Fb(int n)
    {
        if(n==0 || memo[n])  return memo[n];  //在memo里，直接return

        memo[n] = my_Fb(n-1) + my_Fb(n-2);  //不在memo里，先算好存里面，再return
        return memo[n];
    }
};

解法3

递推(动态规划思想) 【自底向上】

递推图：

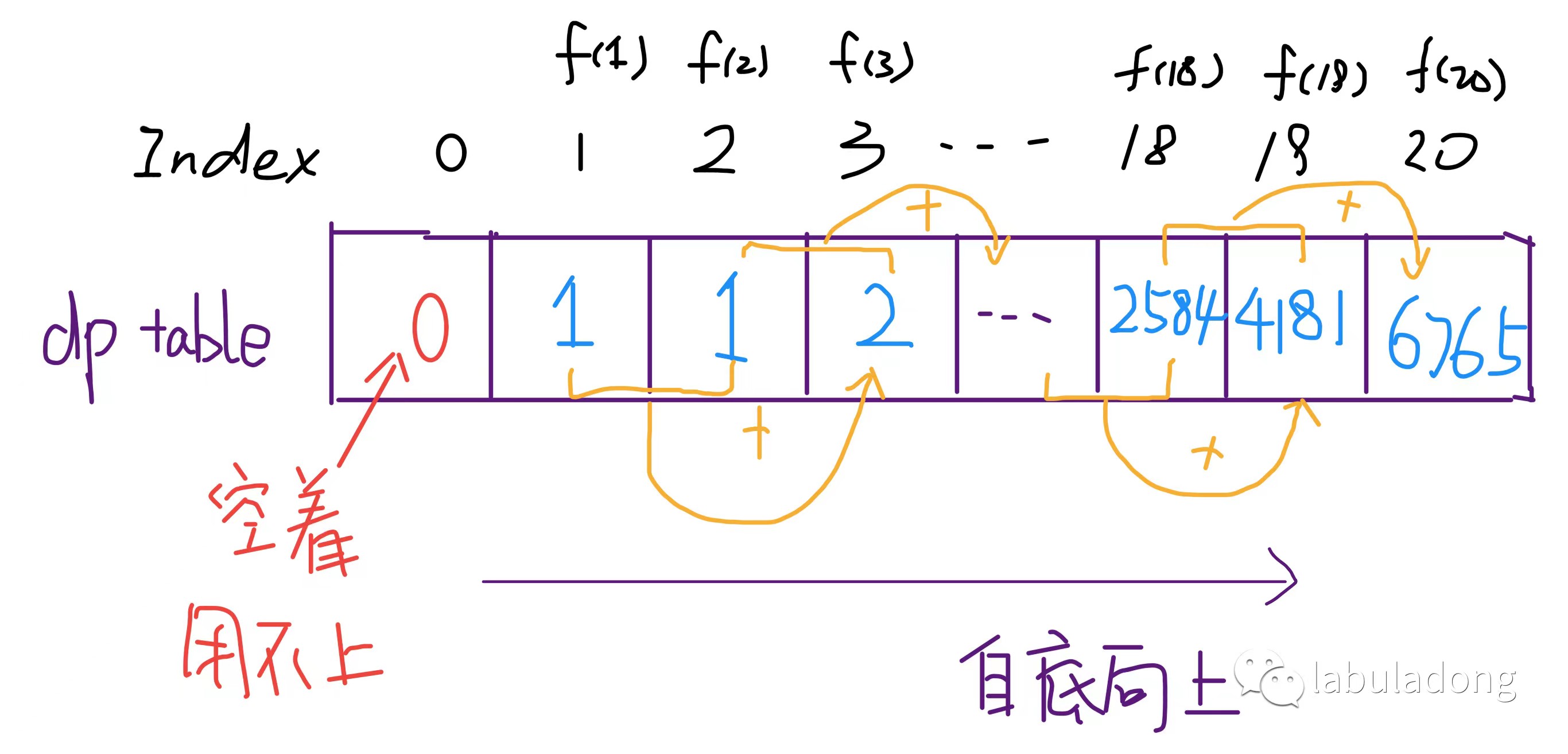
时间复杂度

$O(n)$

参考文献

labuladong

C++ 代码

class Solution {
public:
    int Fibonacci(int n) {
        int a[42];
        a[0]=0,a[1]=1;
        for(int i=2;i<=n;i++)
        {
            a[i]=a[i-1]+a[i-2];  //递推核心式子，即状态转移方程
        }
        return a[n];
    }

};

算法3的优化：

根据递推代码，发现当前状态只和前两个状态有关，只需要存储前两个状态即可，可以将时间复杂度降为O(1)

C++代码

class Solution {
public:
    int Fibonacci(int n) {
        if(n<2)  return n;

        int pre_a = 0 , pre_b = 1;
        int sum;
        for(int i=2;i<=n;i++)
        {
            sum = pre_a + pre_b;  //只记录两个变量及其和，并且时刻更新这两个变量
            pre_a = pre_b;
            pre_b = sum;
        }
        return sum;
    }
};