C++

$\color{#cc33ff}{— > 算法基础课题解}$

$\color{gold}{— > 蓝桥杯辅导课题解}$

思路：

dp

$分析：$

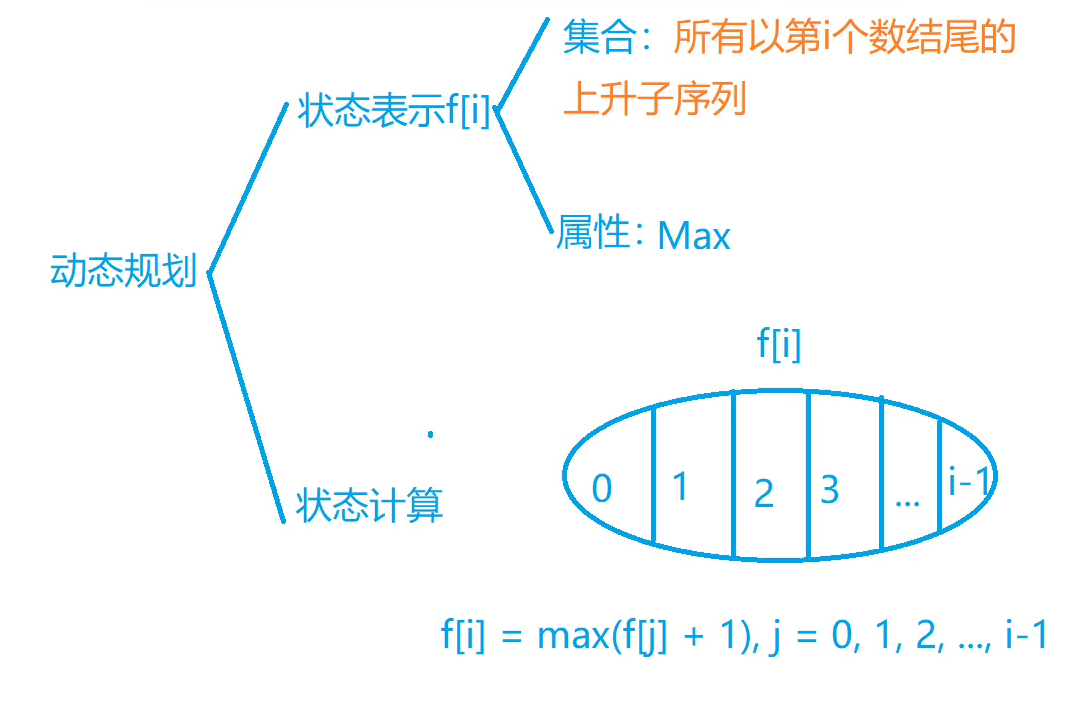
最长上升子序列问题：    

                                        闫氏DP分析法


                        集合：所有以a[i]结尾的严格单调上升子序列

            状态表示
             f[i]
                        属性：max
动态规划 


            状态计算                        f[i](表示所有以a[i]结尾的上升子序列)
                            a[1]    a[2]    a[3]    ···     a[i-1]      空
划分依据：最后一个不同的点                        
                           f[1]+1           f[3]+1  ···                  1
                                        取max

时间复杂度：$O（n^2）$
$code1:$

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N], f[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];

    for (int i = 1; i <= n; i ++) {
        f[i] = 1; // 只有a[i]一个数
        for (int j = 1; j < i; j ++)
            if (a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0;
    for (int i = 1; i <= n; i ++) res = max(res, f[i]);

    cout << res;
    return 0;
}

$code2:$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];

    int res = 0;
    for (int i = 1; i <= n; i ++) {
        f[i] = 1;
        for (int j = 1; j < i; j ++)
            if (a[j] < a[i])
                f[i] = max(f[i], f[j] + 1); // 状态转移

        res = max(res, f[i]);        
    }

    cout << res;

    return 0;
}