AcWing 285. 没有上司的舞会

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 285. 没有上司的舞会原题链接简单

作者：

洛喑 , 2022-03-26 22:06:27 , 所有人可见 , 阅读 11850

529

68

<— ~~麻烦点亮一下旁边这个好看的向上的三角形~~

题目描述

$Ural$ 大学有 $N$ 名职员，编号为 $1∼N$。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 $H_i$ 给出，其中 $1≤i≤N$。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式

第一行一个整数 $N$。

接下来 $N$ 行，第 $i$ 行表示 $i$ 号职员的快乐指数 $H_i$。

接下来 $N−1$ 行，每行输入一对整数 $L,K$，表示 $K$ 是 $L$ 的直接上司。

输出格式

输出最大的快乐指数。

数据范围

$1≤N≤6000$,
$−128≤H_i≤127$

输入样例：

输出样例：

题意简化

~~这道题题目看上去花里胡哨的，但其实挺好理解的~~
前$N$行表示第$i$号职工的快乐指数
后面的$N - 1$行输入两个整数$L,K$，表示 $K$ 是 $L$ 的直接上司，如图。
搜狗截图20220326205220.png
要求使得所有参会职员的快乐指数总和最大。

在这儿讲解一下样例

根据这个样例，我们可以画出一张图（如果还不知道样例是什么意思的看上面），如下：

新建画布1.png

那输出样例的 $5$ 是怎么来的呢？
请看：

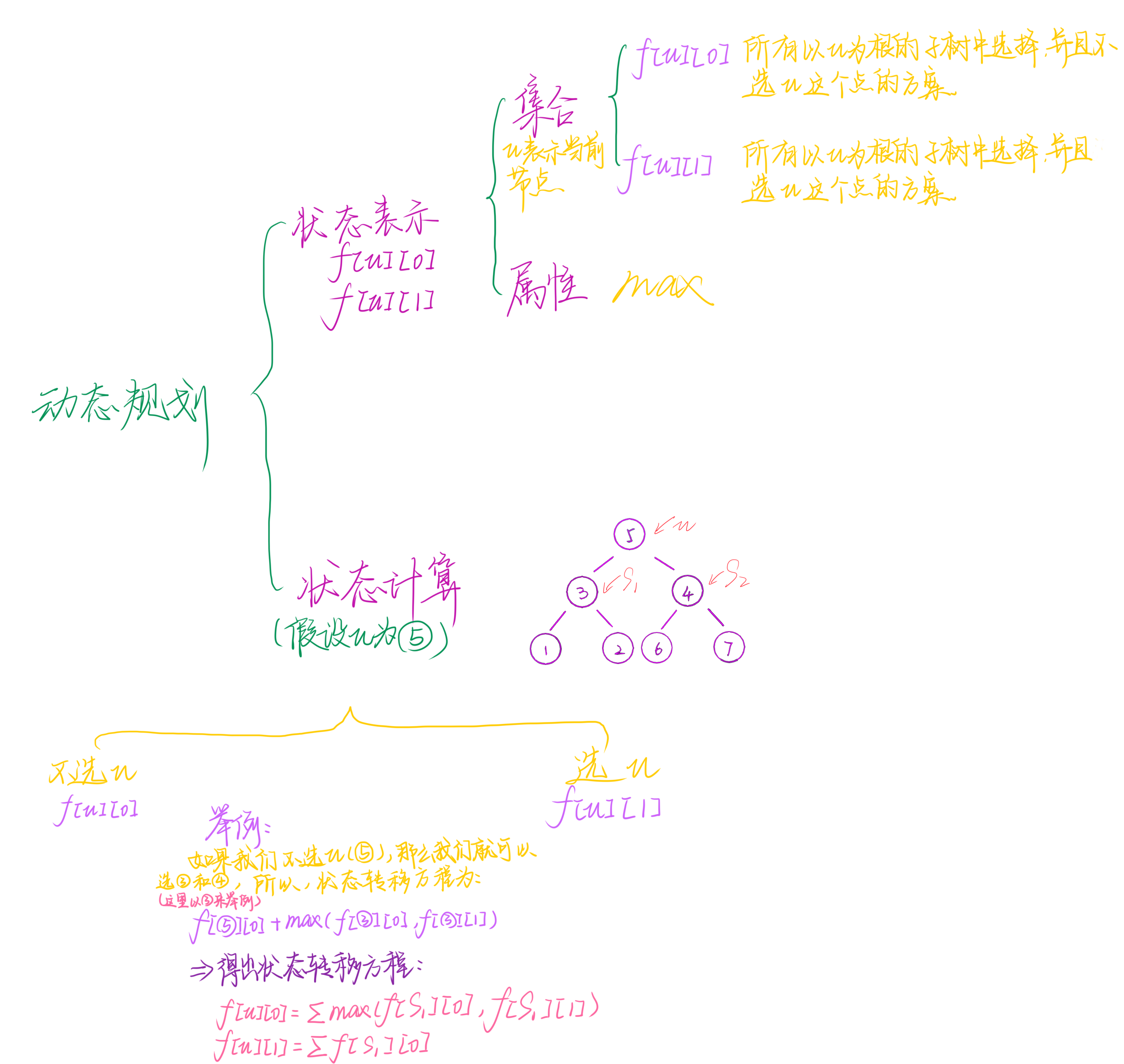
根据画图得出，$⑤$ 是根节点（校长）。
我们知道样例中每个节点的快乐值都为 $1$，所以决定最大快乐值的是节点的数量

在这个样例里，我们必须选校长，为什么呢？
比如我们选了 $③$，那他的下属全部$KO$，或者选了 $④$，也是一样
那我们的最大快乐值就变成了 $3$，错误
只有我们选了 $⑤$，那剩下的 $①$、 $②$、 $⑥$、 $⑦$才能苟活被选中

我们现在选了 $⑤$，那我们就可以有五个人参加，且快乐值是最大的，为 $5$，选中的清晰，如图：

新建画布1.png

发现什么了吗？

当不选 $i$ 节点时，影响最大高兴值的节点为$i$的子节点或其他节点
当选 $i$ 节点时，影响最大高兴值的节点只为$i$的子节点

由此我们可以得出状态转移方程：

当 $f[i][1]$ 时表示选 $i$ 号节点。

那么很明显 $i$ 号节点的快乐值需要算上
然后我们知道，如果选了这个点，它的所有字节点都是不能选的，所以我们应该给它加上 $f[j][0]$
当 $f[i][0]$ 时表示不选 $i$ 号节点。

这时我们不需要加上 $i$ 号点的快乐值
如果不选这个点，它的子节点可以选也可以不选，所以我们应该给它加上 $max{f[j][0],f[j][1]}$

弱弱地问一句，题目看懂并理解了吧…

算法1

(树形DP) $O(n)$

看图：

新建画布1.png

时间复杂度

参考文献

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 6010;
int n;
int happy[N]; //每个职工的高兴度
int f[N][2]; //上面有解释哦~
int e[N],ne[N],h[N],idx; //链表，用来模拟建一个树
bool has_father[N]; //判断当前节点是否有父节点
void add(int a,int b){ //把a插入树中
    e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
void dfs(int u){ //开始求解题目
    f[u][1] = happy[u]; //如果选当前节点u，就可以把f[u,1]先怼上他的高兴度
    for(int i = h[u];~i;i = ne[i]){ //遍历树
        int j = e[i];
        dfs(j); //回溯
        //状态转移部分，上面有详细讲解~
        f[u][0] += max(f[j][1],f[j][0]);
        f[u][1] += f[j][0];
    }
}
int main(){
    scanf("%d",&n);
    for(int i = 1;i <= n;i ++) scanf("%d",&happy[i]); //输入每个人的高兴度
    memset(h,-1,sizeof h); //把h都赋值为-1
    for(int i = 1;i < n;i ++){
        int a,b; //对应题目中的L,K,表示b是a的上司
        scanf("%d%d",&a,&b); //输入~
        has_father[a] = true; //说明a他有上司
        add(b,a); //把a加入到b的后面
    }
    int root = 1; //用来找根节点
    while(has_father[root]) root ++; //找根节点
    dfs(root); //从根节点开始搜索
    printf("%d\n",max(f[root][0],f[root][1])); //输出不选根节点与选根节点的最大值
    return 0;
}

$$共190行$$

107 评论

123go 2022-07-14 17:59

一位蒟蒻AC之后兴高采烈地准备发题解并写好了注释然后看见大佬的题解就%%%%%%并弱弱地附上非官方代码注释补全

#include<bits/stdc++.h>//STL头文件 
using namespace std;//标准化标识符可见范围 
const int N = 10010;//数据规模 
int e[N],ne[N],h[N],idx;//单链表，详见add  <公司人际关系> 
int happy[N];//存快乐值 
int n;//有n个人 
bool has_fa[N];//判断某人有没有上司 
int f[N][2];
//f[u][1]:以u为根节点的子树并且包括u的总快乐指数，
//f[u][0]:以u为根节点并且不包括u的总快乐指数;
void add(int a,int b)//邻接表建图 
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx,idx++;  
}
//节点的编号是指上图所画的树中节点的值，范围是从1~n。在本题中，每次输入的a和b就是节点的编号，编号用e[i]数组存储。
//节点的下标指节点在数组中的位置索引，数组之间的关系就是通过下标来建立连接，下标用idx来记录。idx范围从0开始，如果idx==-1表示空(公司里全是鬼)-->新算法题《人都没有的舞会》。
//ne[i]的值是下标，是下标为i的节点的next节点的下标，ne[i]=-1表示该表已被遍历完。
//h[i]存储的是下标，是编号为i的节点的next节点的下标，表示以i为头节点的子树。
void dfs(int u)//递归每一个点 ，u为点的编号 
{
    f[u][1]=happy[u];//该boss要来，此时快乐值至少为该boss的快乐值 
    for(int i=h[u]/*取出头节点*/;i!=-1/*一直找到这条单链表为空*/;i=ne[i]/*下一个与u所连点的下标，实现遍历*/)//从头节点开始遍历邻接表 
    {
        int j=e[i];//取出相连点所存的值 （点的编号） 
        dfs(j);//用该值开始新遍历
        f[u][1]+=f[j][0];//u是j的上司，存在领导关系，所以一定不能让j来<boss归来，小弟承让> 
        f[u][0]+=max(f[j][0],f[j][1]);//u可以作为j和u的上司的中间人，j来不来都可以 <boss不在，小弟为王，小弟来与否？> 
    }
    //这里可以不写return，上方循环肯定不是死循环且遍历终有尽时，在一切执行完之后自动return 
}
int main()//主函数 
{
    scanf("%d",&n);//输入n<舞会积极报名中> 
    for(int i=1;i<=n;i++) cin>>happy[i];//输入快乐值 
    memset(h,-1,sizeof h);//头节点数组初始化为-1（每个点都无相连接的点） 
    for(int i=n+1;i<2*n;i++)
    {
        int a,b;//a是b的上司 
        scanf("%d %d",&b,&a);//输入上司关系 
        has_fa[b]=true;//确认b有上司<是个打工人> 
        add(a,b);//加边建树 
    }
    int root=1;//赋头节点初值（最小为1（公司至少有一个人吧）） 
    while (has_fa[root])root++;//找到没有上司的节点，即为根节点<公司大boss> 
    dfs(root);//从根节点开始dfs遍历 
    printf("%d\n", max(f[root][0],f[root][1]));//比较头节点的两种方案 <大oss到底来不来好>
    //<舞会的开始> 
    return 0;//结束程序 <舞会的结束> 
}