初赛 NOIp2017








单项选择题
1.C 2022 详情看官网
2.B 首位0、1分别表示正、负,正数的反码是它本身,负数的反码是它原码除符号位外按位取反;正数的补码是它本身,负数的补码是它的反码+1,所以题目中补码的原码为11010101,符号位为1表示这是个负数
3.A
分辨率为1600900表示有1600900=1440000个像素,每个像素是16位,所以有1440000*16=23040000bit=2880000B=2812.5KB
4.C 刚过了国庆节 qaq
5.A 树的定义<>
6.C n/2 是以log的速度下降 再带个 数 很明显是log²
7.B 每年一道
8.C
4个不同点构成简单无向连通图,最多有4*(4-1)/2=6 条边(强联通图),最少有4-1=3 条边(树),但注意,不是所有的任选3条边都满足条件,有一种情况是三个点形成一个三角形而孤立一个点,这种情况共有4种
所以 ans=C(6,3)-4+C(6,4)+C(6,5)+C(6,6)=38
9.D 隔板法 详情 请看我讲课
10.B 在视频说8
11.D 常识题
12.D
看懂注释就很简单了..if W(x)<>W(y) 说明不是不合格的不是在X就是在Y 所以是a else不合格的在Z里所以b,A已经更新,所以下一步更新n,所以是c..
这个题干其实是一个很经典的面试题来着…
-
A 数字三角形?
-
D
1-(0.10.8)-(0.20.9)= 0.74
15.C
一共有2603=360个球
360/20=18(个)
不定选择题
1.CD
冒泡最坏O(n^2),快排最坏O(n^2)退化成冒泡,归排和堆排最好最坏都是O(nlog2n)
2.C
栈,先进先出..所以d进去出来后,下一个出来的是c不是b
3.D
haishipaixu
4.BD 5555这也太显然了8
5.BD
奥斯卡 什么鬼
三
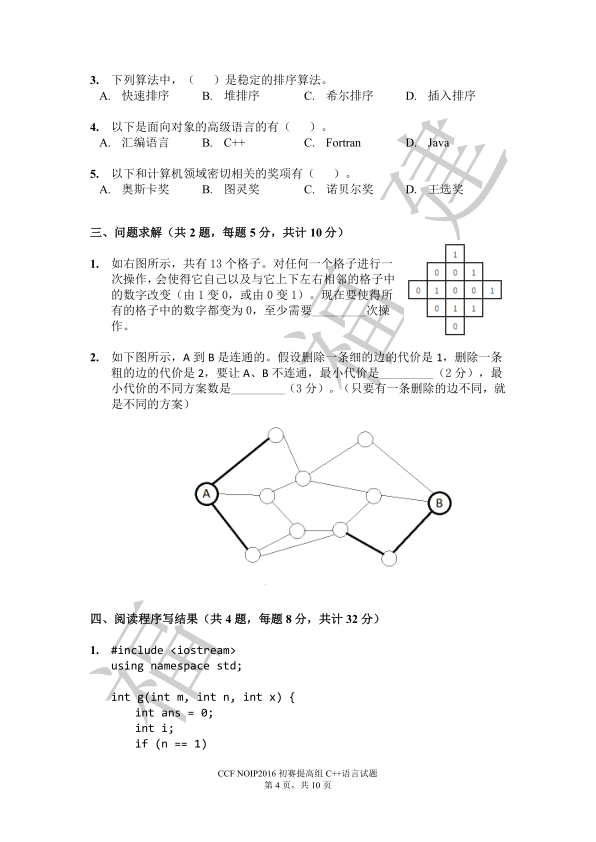
1、3
第一次:第三排右数第二个
第二次:第四排中间那个
第三次:最上面那个
2、4 9
裸的最小割转对偶图..
其实上面那个不会也没有关系,想让AB不连通的最小代价只要把直接连B的三条边断掉就行(1+1+2=4),不同方案的话就拿着4去试就行…
四、
1、15
跟着跑就行..
g(8,4,0)=g(8,3,0)+g(7,3,1)+g(6,3,2)=10+4+1=15
g(8,3,0)=g(8,2,0)+g(7,2,1)+g(6,2,2)=5+3+2=10
g(8,2,0)=g(8,1,0)+g(7,1,1)+g(6,1,2)+g(5,1,3)+g(4,1,4)=5
g(7,2,1)=g(6,1,1)+g(5,1,2)+g(4,1,3)=3
g(6,2,2)=g(4,1,2)+g(3,1,3)=2
g(7,3,1)=g(6,2,1)+g(5,2,2)=3+1=4
g(6,2,1)=g(5,1,1)+g(4,1,2)+g(3,1,3)=3
g(5,2,2)=g(3,1,2)=1
g(6,3,2)=g(4,2,2)=g(2,1,2)=1
2、17 24 1 8 15
这就是一个幻方…看出来的直接写,看不出来的按照它给的规则写:第一行中间是1,下一个数写在上一个数的右上面那个格(第一行的上一行是最后一行,最后一列的右面是第一列),如果右上面那个格已经填过就填它下面那个(能填右上填右上,填不了右上就填右面那个)
3、8
这就是在数逆序对
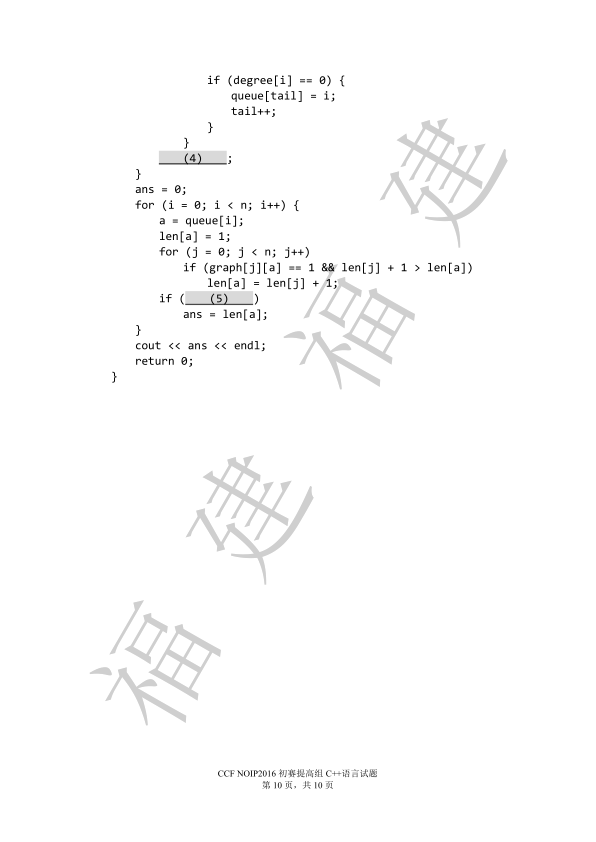
4、 1 3
2017 1
1 321
矩阵内45度反弹…到哪个角就是那个…

