什么是 $A*$ (A-star) 算法

A-star 算法在图上为点定义了估价函数 $f(x)$，表示 $x$ 到终点的估计距离，并且保证 $f(x) \leqslant g(x)$（其中 $g(x)$ 表示点 $x$ 到终点的真实距离），由此，我们可以使用优先队列维护 $d(x)+f(x)$ （其中 $d(x)$ 表示起点到点 $x$ 的真实距离），每次取出最小值，用其点更新其他节点，并入队。那么终点第一次出队时，就是最短路。
补充：A-star 实质就是剪枝的搜索。

证明：

反证法，假设不是最短路，即存在从起点到终点的另一个路径，其长度 $d < d(t)$ ，其中 $t$ 是终点（注意到终点到终点的估价 $f(t)=0$）。又最优解路径上一定有点在优先队列中，不放设其中一个点为 $u$，则 $d(t)=d(t)+f(t) > d=d(u)+g(u) \geqslant d(u)+f(u)$，即有 $d(t)+f(t) > d(u) + f(u)$，这与算法中 $d(t)+f(t)$ 是队列中最小值矛盾，故假设不成立，原命题成立。

八数码

设计估价函数 $f(str)$ 表示当前状态 $str$ 中每个数和它的目标位置的曼哈顿距离之和，即可满足估价函数的性质，因为每个数只有在最优情况下才可能直接平移曼哈顿距离次。
需要注意的是，当问题无解时，带有 A-star 的搜索会退化，因此需要判断无解情况，这里不给出证明了（我不会）。
文章最后给出一种变换到 $12345678x$，输出变换操作数和过程的代码。
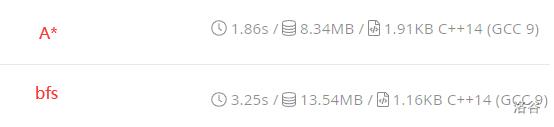
与普通 BFS 的对比：

k 短路

类似于关于最短路的证明，我们可以证明，终点 $t$ 第 $k$ 次弹出时对应的 $d(t)$ 一定是第 $k$ 短路。
至于估价函数的构造，我们可以直接采用点 $u$ 到终点的最短路长度，可以用 dijkstra 预处理。

习题

Cow Jogging G
关于 A* 的题好像并不多

CODE

八数码

#include <iostream>
#include <queue>
#include <string>
#include <cmath>
#include <unordered_map>
#include <vector>
#include <algorithm>
#define PSS pair<string, string>
#define PIP pair<int, PSS>
#define x first
#define y second.first
#define z second.second

using namespace std;

// 估价函数
int f(string state)
{
    int ans = 0;
    for (int i = 0; i < 9; i ++ )
    {
        if (state[i] == 'x')
            continue;
        int t = state[i] - '1';
        int truex = t / 3, truey = t % 3;
        int nwx = i / 3, nwy = i % 3;
        ans += abs(nwx - truex) + abs(nwy - truey);
    }
    return ans;
}

void Astar(string start)
{
    string end = "12345678x";

    int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
    char dc[4] = {'r', 'l', 'd', 'u'};
    unordered_map<string, int> dist;
    priority_queue<PIP, vector<PIP>, greater<PIP>> heap;

    dist[start] = 0;
    heap.push({f(start), {start, ""}});
    while (heap.size())
    {
        PIP t = heap.top(); heap.pop();
        int d = t.x;
        string state = t.y, ans = t.z;

        if (state == end)
        {
            cout << dist[state] << "\n";
            cout << ans;
            return;
        }

        int k = state.find('x');
        int a = k / 3, b = k % 3;
        for (int i = 0; i < 4; i ++ )
        {
            int xx = a + dx[i], yy = b + dy[i];
            if (xx < 0 || xx > 2 || yy < 0 || yy > 2)
                continue;

            string nw = state;
            swap(nw[a * 3 + b], nw[xx * 3 + yy]);

            if (!dist.count(nw) || dist[nw] > dist[state] + 1)
            {
                dist[nw] = dist[state] + 1;
                heap.push({f(nw) + dist[nw], {nw, ans + dc[i]}});
            }

        }
    }
    return;
}

int main()
{
    string start;
    char ch;
    int cnt = 0;

    while (cin >> ch)
    {
        for (int i = 0; i < start.size(); i ++ )
            if (start[i] > ch && start[i] != 'x' && ch != 'x')
                cnt ++;
        start += ch;
    }

    // 判断无解
    if (cnt & 1)
        puts("unsolvable");
    else Astar(start);

    return 0;
}

k 短路

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#include <vector>
#define PII pair<int, int>
#define PIP pair<int, PII>

using namespace std;

const int N = 1010, M = 2e4 + 10;

// rh 为反边，用于 dijkstra 求估价
int h[N], rh[N], e[M], ne[M], w[M], idx;
// dist 为估价， cnt[i] 为 i 出队的次数，如此省略不必要的运算。
// 特殊地，cnt[t] 的值代表当前出队的终点对应 d 是第几短路。
int dist[N], cnt[N];
bool st[N];
int n, m, s, t, k;

void add(int h[], int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

// 求终点到每个点的最短路，即估价函数
void dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[t] = 0;

    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, t});

    while (heap.size())
    {
        int u = heap.top().second; heap.pop();

        if (st[u])
            continue;
        st[u] = true;

        for (int i = rh[u]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[u] + w[i])
            {
                dist[j] = dist[u] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    return;
}

int Astar()
{
    priority_queue<PIP, vector<PIP>, greater<PIP>> heap;
    heap.push({dist[s], {0, s}});

    while (heap.size())
    {
        PIP nw = heap.top(); heap.pop();
        int u = nw.second.second, d = nw.second.first;

        cnt[u] ++;
        if (cnt[t] == k)
            return d;

        for (int i = h[u]; ~i; i = ne[i])
        {
            int j = e[i];
            if (cnt[j] < k)
                heap.push({dist[j] + d + w[i], {d + w[i], j}});
        }
    }
    return -1;
}

int main()
{
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);

    cin >> n >> m;
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(h, a, b, c);
        add(rh, b, a, c);
    }

    cin >> s >> t >> k;
    // 题目要求
    if (s == t) k ++;

    dijkstra();

    cout << Astar();

    return 0;
}