关于树链剖分(重链剖分+长链剖分)
重链剖分:
·重儿子:每个点的子树中,子树的节点数和最大的子节点
·轻儿子:除重儿子外的其他子节点
·重边:每个节点与其重儿子间的边
·轻边:每个节点与其轻儿子间的边
·重链:重边连成的链 (一个点也可以看作是重链)
·轻链:轻边连成的链
如下图:
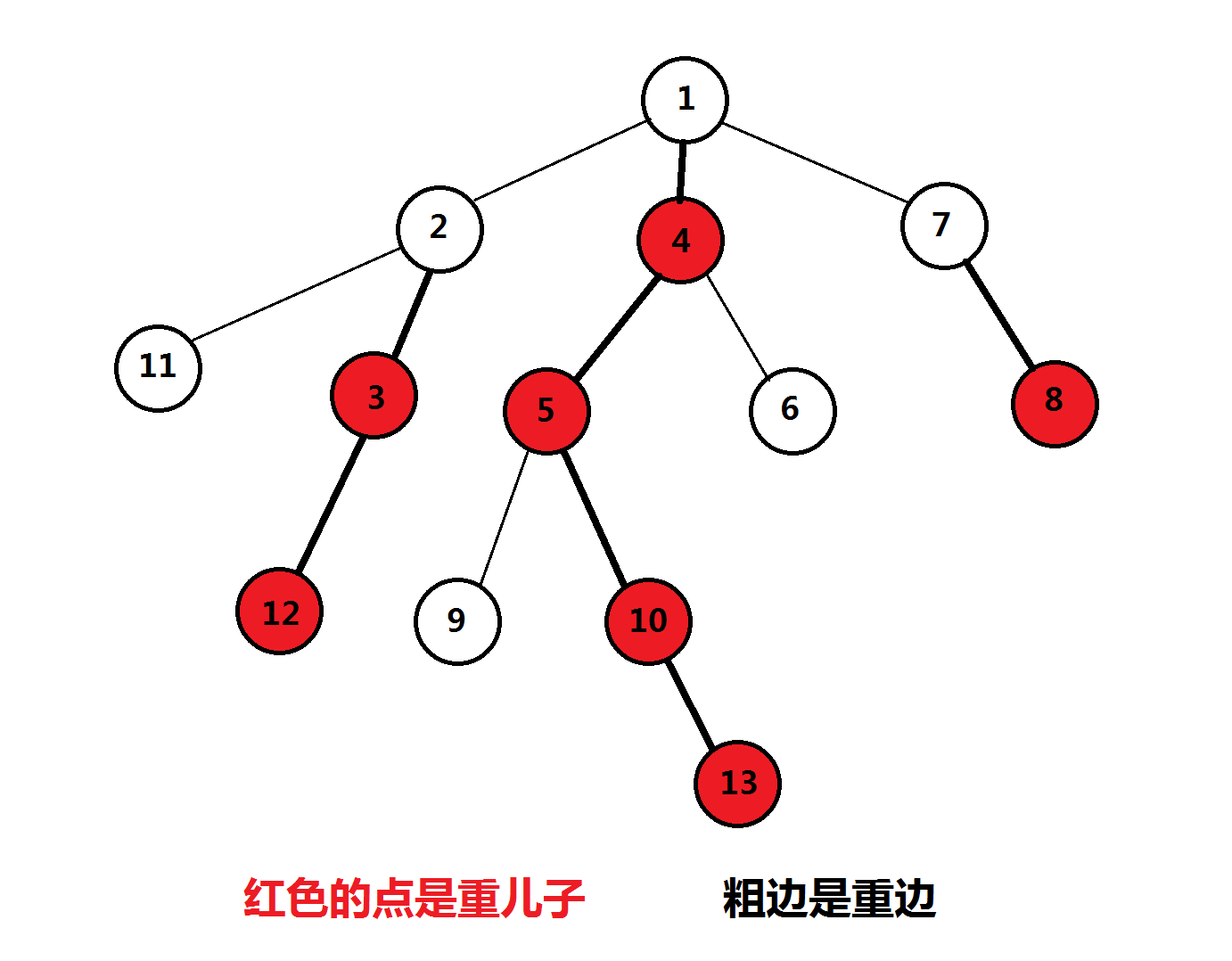
很明显,一棵树可以被剖分成若干个无交集的重链,而剖分的过程就叫做重链剖分
重链剖分的实现:
两次 dfs
第一次 dfs:处理出每个点的重儿子,子树的节点数和,深度,父节点
关于重儿子,子树节点数和处理的实现:先深搜,在回溯时记录
第二次 dfs:处理出每个点所在重链的链头
深搜时,如果搜到重儿子,链头不变;搜到轻儿子,链头改成轻儿子就行了
代码实现:
const int N=500000+10;
int wson[N], size[N], fa[N], dep[N], top[N];
// 重儿子 子树节点数和 父节点 节点深度 链头
int head[N],ver[N*2],nex[N*2];
void dfs1(int x)
{
size[x]=1;
dep[x]=dep[fa[x]]+1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
size[x]+=size[y];
if(size[y]>size[wson[x]]) wson[x]=y;
//回溯时更新子树节点和、重儿子
}
}
}
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(wson[x]) dfs2(wson[x],nowtop);
//重儿子链头不变
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x]&&y!=wson[x]) dfs2(y,y);
//轻儿子代表一条新的重链,链头为轻儿子
}
}
重链剖分的一些性质:
·所有重链互不相交,每个点只属于一条重链
·所有重链长度和等于节点数
·一个点到根节点的路径上经过的边中轻边最多只有 log 条(重儿子和轻儿子节点数和相等时取到)
重链剖分的用处:
·O(1) 移动到链头 (求 lca)
·直接修改或查询重链上的信息 (结合线段树)
重链剖分求 lca 的实现步骤:
1) 将两点中链头更深的点跳到链头
2) 若两点不在同一重链上,更深点跳转到父节点
3) 重复操作 1)、2)直到两点处于同一条重链上,此时深度较浅的点即为所求
关于 3) 的证明:
很明显当两点处于同一条重链上时,它们的父节点也处于这条重链上,并且这个父节点,就是这两点中深度较浅的点。
代码实现:
#include<bits/stdc++.h>
using namespace std;
const int N=500000+10;
int wson[N],size[N],fa[N],dep[N],top[N];
int head[N],ver[N*2],nex[N*2];
int n,m,tot=0,root=1; //一般根节点为 1
void add(int x,int y)
{
ver[++tot]=y;
nex[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
size[x]=1;
dep[x]=dep[fa[x]]+1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
size[x]+=size[y];
if(size[y]>size[wson[x]]) wson[x]=y;
}
}
}
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(wson[x]) dfs2(wson[x],nowtop);
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x]&&y!=wson[x]) dfs2(y,y);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
//将所在链的链头更深的点跳到链头
}
return dep[x]<dep[y]?x:y;
//返回深度更浅的点
}
int main()
{
scanf("%d%d%d",&n,&m,&root);
//scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;++i)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(root);
dfs2(root,root);
//根节点为最长长链的链头
for(int i=1,x,y;i<=m;i++)
{
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}
长链剖分:
·长儿子:子树深度最大的子节点
·短儿子:除长儿子外的子节点
·长边:每个节点与长儿子间的连边
·短边:每个节点与短儿子间的连边
·长链:长边构成的链
·短链:短边构成的链
如下图:
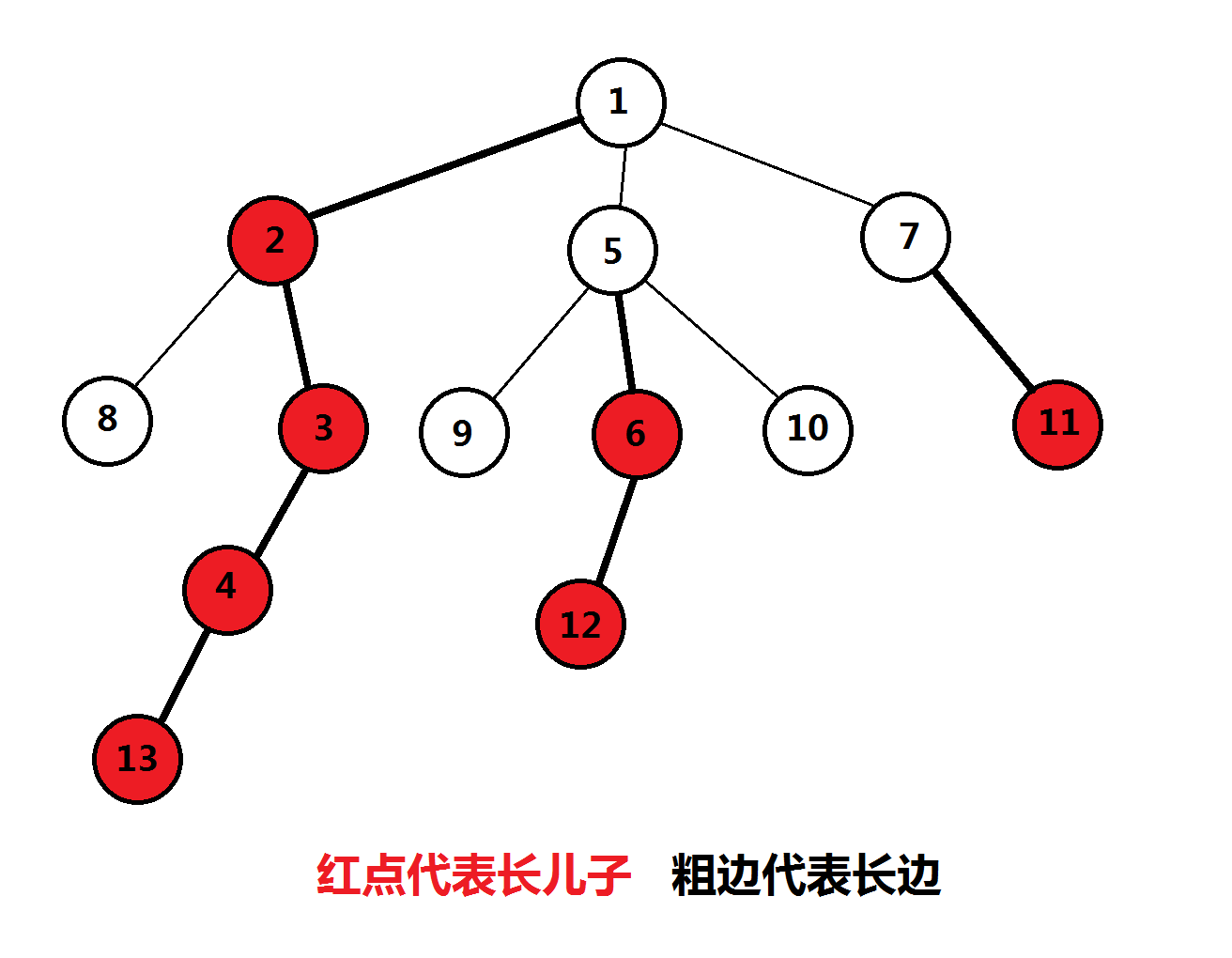
与重链剖分一样,一棵树被分成若干个无交集的长链,叫长链剖分
长链剖分的实现:与重链剖分类似,也是两次 dfs
代码实现:
const int N=500000+10;
int lson[N],maxlen[N], fa[N], dep[N], top[N];
// 长儿子 子树深度 父节点 节点深度 链头
int head[N],ver[N*2],nex[N*2];
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
maxlen[x]=dep[x];
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
maxlen[x]=max(maxlen[y],maxlen[x]);
if(maxlen[y]>maxlen[lson[x]]) lson[x]=y;
//回溯时更新子树深度和长儿子
}
}
}
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(lson[x]) dfs2(lson[x],nowtop);
//长儿子链头不变
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x]&&y!=lson[x]) dfs2(y,y);
//短儿子代表一条新的长链,链头为短儿子
}
}
长链剖分的性质:
长链剖分有比重链剖分更好的性质
·任意点祖先所在长链长度一点大于等于这个点所在长链长度
·所有长链长度之和就是总结点数
·一个点到根节点的路径上经过的短边最多有 √n 条 (长儿子深度和短儿子深度相等时取到)
长链剖分的用处:
·O(1) 移动到链头 (求lca,和重链剖分一样)
·O(nlogn) 预处理,单次 O(1) 在线查询一个点的 k 级祖先
·O(n) 处理可合并的与深度有关的子树信息 (例如某深度点数、某深度点权和)
长链剖分求 lca 的代码实现:
#include<bits/stdc++.h>
using namespace std;
const int N=500000+10;
int lson[N],maxlen[N],fa[N],dep[N],top[N];
int head[N],ver[N*2],nex[N*2];
int n,m,tot=0,root=1;
void add(int x,int y)
{
ver[++tot]=y;
nex[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
maxlen[x]=dep[x];
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
maxlen[x]=max(maxlen[y],maxlen[x]);
if(maxlen[y]>maxlen[lson[x]]) lson[x]=y;
}
}
}
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(lson[x]) dfs2(lson[x],nowtop);
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x]&&y!=lson[x]) dfs2(y,y);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
int main()
{
scanf("%d%d%d",&n,&m,&root);
//scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;++i)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(root);
dfs2(root,root);
for(int i=1,x,y;i<=m;++i)
{
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}
关于在线求 k 级祖先的实现:
1) 暴力预处理出每个链头往上链长个祖先及这条链上所有的点,再预处理出所有二进制的最高次幂
2) 查询祖先时,先跳能跳的 2 的最高次幂,再在所在链的链头上 O(1) 查询祖先
关于 2) 的证明:
我们由长链的性质得,点 x 往上跳 k/2 个点到达的长链深度一点大于 k/2 ,也就是链的长度一定大于 k/2
所以无论 x 的 k 级祖先在原先链上
还是在点 x 的 2 的最高次幂祖先所在的链上
还是在点 x 的 2 的最高次幂祖先所在的链的链头上方
都在我们预处理的范围内,就都能做到 O(1) 求出祖先了
代码实现:
#include<bits/stdc++.h>
using namespace std;
const int N=500000+10;
int lson[N],maxlen[N],fa[N],dep[N],top[N];
int head[N],ver[N*2],nex[N*2];
int f[N][22],st[N*2];
vector<int> up[N],down[N];
int n,m,tot=0,root=1;
void add(int x,int y)
{
ver[++tot]=y;
nex[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
maxlen[x]=dep[x];
f[x][0]=fa[x];
for(int i=1;i<=19;i++)
{
if(f[x][i-1]) f[x][i]=f[f[x][i-1]][i-1];
else break;
}
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
maxlen[x]=max(maxlen[y],maxlen[x]);
if(maxlen[y]>maxlen[lson[x]]) lson[x]=y,maxlen[x]=maxlen[y];
}
}
}
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(lson[x]) dfs2(lson[x],nowtop);
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y!=fa[x]&&y!=lson[x]) dfs2(y,y);
}
}
void chain_prework(int x) //预处理
{
int rot=x,len=maxlen[x]-dep[x];
//rot 为链头,len 为链长
x=fa[rot];
while(dep[rot]-dep[x]<=len&&x)
{
up[rot].push_back(x);
x=fa[x];
//处理链头上方链长个点
}
x=rot;
while(lson[x])
{
down[rot].push_back(lson[x]);
x=lson[x];
//处理链中的点
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;++i)
{
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs1(root);
dfs2(root,root);
st[1]=0;
for(int i=2;i<=n;++i) st[i]=st[i>>1]+1;
for(int i=1;i<=n;++i)
if(i==top[i]) chain_prework(i);
for(int i=1,x,y;i<=m;++i)
{
int ans=0;
scanf("%d%d",&x,&y);
x=x^ans;
y=y^ans;
if(y==0) ans=x;
else if(y>=dep[x]) ans=0;
else
{
x=f[x][st[y]];
y-=(1<<st[y]);
//先跳能跳的 2 的最大次幂
if(y==0) ans=x;
else if(y<dep[x]-dep[top[x]]) ans=down[top[x]][dep[x]-dep[top[x]]-y-1];
//在链中
else if(y==dep[x]-dep[top[x]]) ans=top[x];
//在链头
else ans=up[top[x]][y-dep[x]+dep[top[x]]-1];
//在链上方
}
printf("%d\n",ans);
}
return 0;
}


👍
谢( ̄▽ ̄)~
赞!
谢( ̄▽ ̄)