前言

树上莫队可以在树上查询一些很有意思的东西，比如众数、数的出现次数。
在阅读这篇文章之前，请确保你会基本的莫队以及欧拉序。

一些概念

众所周知莫队是在序列上进行一系列的查询的，并且必须离线与静态（当然后人也发明出了带修莫队与在线莫队）。那么我们就不妨考虑将一棵树转为一个序列，再在这个序列上进行我们想要的操作。
这个序列就是欧拉序。

树上莫队

以这张图为我们的树，比如每次查询从u到v的路径。

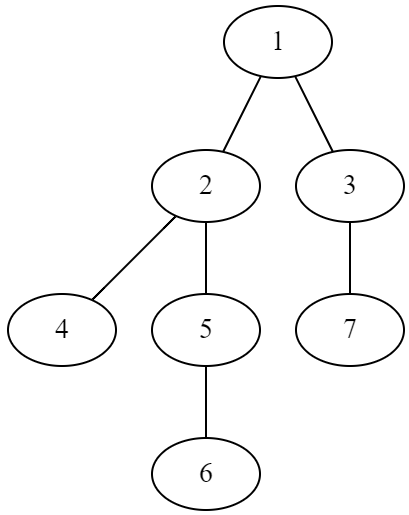
如果以1为根，欧拉序为1 2 4 4 5 6 6 5 3 7 7 3 1
那么每次询问就要把ein小的点放在前面，这样才好进行查询。
写成代码即

if(ein[u]>ein[v])
  swap(u,v);

这样就保证了u和v在欧拉序上是有序的。
我们分两种路径关系来讨论。

直线型路径

就是一个点是另一个点的祖先的路径称为直线型路径（因为在树上是一条直线，比如从1–5）。
对于直线型路径，我们可以将其看做是[ein[u],ein[v]]这个序列的区间。
区间内有许多出现了两次的点，那么出现两次我们就不把它统计进去就好了。

折线型路径

如果两个点没有任何关系，lca不为两个点其中之一。那么我们将它看做是[eout[u],ein[v]]这个区间。与直线型相同，出现两次的点不统计。
但是。。。我们没有统计LCA？怎么办？
统计进去就行了呗。
可以对着上面那张图模拟一通。

例题&代码

我们虽然知道了树上莫队是什么，但是怎么写出来还是需要一些技巧的。
SP10707 COT2 - Count on a tree II
数颜色，一看就不是什么好东西。
果断选择莫队。
AC代码：

#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;
const int N=5e5+5;
int n,m,col[N]; //点数与询问数 
int b[N];
int head[N],to[N],nxt[N],cnt;   //链式前向星 
int siz,ans[N],res,a[N],pos[N]; //莫队 
int ein[N],eout[N],eular[N],tot;    //欧拉序 
int f[N][21],h,d[N];    //LCA 
bool sgn[N];    //重复访问

struct Q {  //莫队的询问 
    int l,r;
    int idx;
    int anc;
}q[N];

bool cmp(Q a,Q b) {     //压行的排序
    return pos[a.l]==pos[b.l]?pos[a.r]<pos[b.r]:pos[a.l]<pos[b.l];
} 

void add(int u,int v) {
    to[++cnt]=v;
    nxt[cnt]=head[u];
    head[u]=cnt;
}

void dfs(int u,int fa) {    //传统艺能
    f[u][0]=fa;
    for(int i=1;i<=h;i++)
      f[u][i]=f[f[u][i-1]][i-1];
    d[u]=d[fa]+1;
    eular[++tot]=u;
    ein[u]=tot;
    for(int i=head[u];i;i=nxt[i]) {
        int v=to[i];
        if(fa!=v)
          dfs(v,u);
    }
    eular[++tot]=u;
    eout[u]=tot;
} 

bool up(int u,int v) {
    return ein[u]<=ein[v] and eout[u]>=eout[v]; //传统艺能 
}

void update(int x) {    //莫队的更新结点
    if(sgn[x])  //如果这个点被更新过
      res-=(--a[col[x]]==0);
    else
      res+=(++a[col[x]]==1);
    sgn[x]^=1;  //取反
}

int lca(int x,int y) {  //传统艺能
    if(up(x,y))
      return x;
    if(up(y,x))
      return y;
    for(int i=h;i>=0;i--)
      if(!up(f[x][i],y) and f[x][i]!=0)
        x=f[x][i];
    return f[x][0];
}

int main() {
    //这边都用的是c输入输出，因为这题太卡常
    scanf("%d%d",&n,&m);
    siz=sqrt(m)+1;  //每块大小
    h=log(n)/log(2)+1;  //树高度
    for(int i=1;i<=n;i++) {
        scanf("%d",&b[i]);
        col[i]=b[i];
    }
    //这里需要离散化，不然桶开不到那么大，我之前就RE了好几次
    sort(b+1,b+n+1);
    for(int i=1;i<=n;i++)
      col[i]=lower_bound(b+1,b+n+1,col[i])-b;
    //建树
    for(int i=1;i<n;i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    //分块
    for(int i=1;i<=2*n;i++)
      pos[i]=i/siz+1;
    dfs(1,0);
    //读入询问
    for(int i=1;i<=m;i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        q[i].idx=i;
        q[i].anc=lca(u,v);  //记录下lca
        if(ein[u]>ein[v])   //将uv变有序
          swap(u,v);
        if(q[i].anc==u) {
            q[i].l=ein[u];
            q[i].r=ein[v];
            q[i].anc=0;     //直线型无需统计lca
        }
        else {
            q[i].l=eout[u];
            q[i].r=ein[v];
        }
    }
    //将询问排序
    sort(q+1,q+m+1,cmp);
    //处理询问
    int l=1,r=0;
    for(int i=1;i<=m;i++) {
        while(q[i].l<l) update(eular[--l]);
        while(q[i].r>r) update(eular[++r]);
        while(q[i].l>l) update(eular[l++]);
        while(q[i].r<r) update(eular[r--]);
        if(q[i].anc) update(q[i].anc);  //折线型没统计LCA
        ans[q[i].idx]=res;
        if(q[i].anc) update(q[i].anc);  //统计完，删掉
    }
    for(int i=1;i<=m;i++)
      printf("%d\n",ans[i]);    //输出
    return 0;
}