$$舞蹈链$$

$引入$

给定$n$个$01$序列

从中选择尽量少的序列

使得每一列恰好有一个$1$（精确覆盖问题）或至少有一个$1$（重复覆盖问题）

这里就需要用$Dacing\ Links$

$十字链表$

对于每一个为$1$的格，表示为一个点

每一行中的$1$的点用$l$，$r$串联

每一列中的$1$的点用$u$，$d$串联

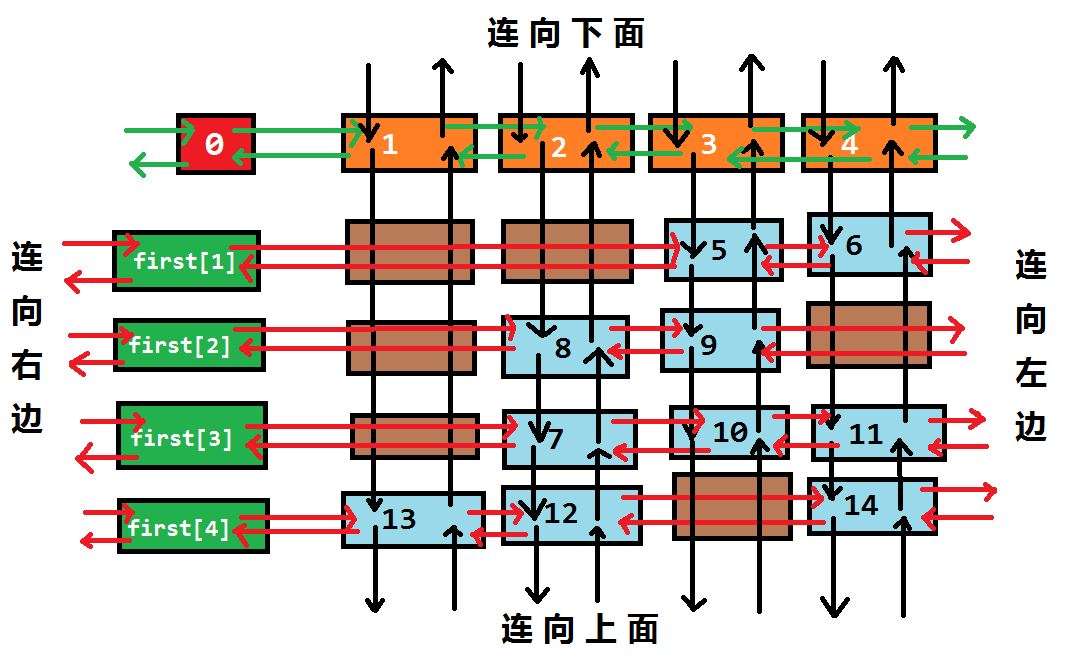
$row[i]$ 为$i$号节点所在行的编号

$col[i]$ 为$i$号节点所在列的编号

$s[y]$ 为第$y$列现有$1$的个数

$精确覆盖问题$

将给定$n$个序列转化成$n$行矩阵

$ \left\( \begin{matrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \\\ \end{matrix} \right\) $

$DLX$ 算法思想和暴力一样：

1.先找到$1$个数少的一列(优化搜索顺序)

这里选第$3$列

$ \left\( \begin{matrix} 0 & 0 & \color{#0000FF}{1} & 0 & 1 & 1 & 0 \\\ 1 & 0 & \color{#0000FF}{0} & 1 & 0 & 0 & 1 \\\ 0 & 1 & \color{#0000FF}{1} & 0 & 0 & 1 & 0 \\\ 1 & 0 & \color{#0000FF}{0} & 1 & 0 & 0 & 0 \\\ 0 & 1 & \color{#0000FF}{0} & 0 & 0 & 0 & 1 \\\ 0 & 0 & \color{#0000FF}{0} & 1 & 1 & 0 & 1 \\\ \end{matrix} \right\) $

2.从这一列所有$1$枚举

这里选择第$3$行

$ \left\( \begin{matrix} 0 & 0 & \color{#0000FF}{1} & 0 & 1 & 1 & 0 \\\ 1 & 0 & \color{#0000FF}{0} & 1 & 0 & 0 & 1 \\\ \color{red}{0} & \color{red}{1} & \color{red}{1} & \color{red}{0} & \color{red}{0} & \color{red}{1} & \color{red}{0} \\\ 1 & 0 & \color{#0000FF}{0} & 1 & 0 & 0 & 0 \\\ 0 & 1 & \color{#0000FF}{0} & 0 & 0 & 0 & 1 \\\ 0 & 0 & \color{#0000FF}{0} & 1 & 1 & 0 & 1 \\\ \end{matrix} \right\) $

3.找出这一行中有$1$的列

$ \left\( \begin{matrix} 0 & \color{green}{0} & \color{#0000FF}{1} & 0 & 1 & \color{green}{1} & 0 \\\ 1 & \color{green}{0} & \color{#0000FF}{0} & 1 & 0 & \color{green}{0} & 1 \\\ \color{red}{0} & \color{red}{1} & \color{red}{1} & \color{red}{0} & \color{red}{0} & \color{red}{1} & \color{red}{0} \\\ 1 & \color{green}{0} & \color{#0000FF}{0} & 1 & 0 & \color{green}{0} & 0 \\\ 0 & \color{green}{1} & \color{#0000FF}{0} & 0 & 0 & \color{green}{0} & 1 \\\ 0 & \color{green}{0} & \color{#0000FF}{0} & 1 & 1 & \color{green}{0} & 1 \\\ \end{matrix} \right\) $

4.将所有有颜色的数删去，得到新的矩阵

$ \left\( \begin{matrix} 0 & 0 & 1 & 0 \\\ 1 & 1 & 0 & 1 \\\ 1 & 1 & 0 & 0 \\\ 0 & 0 & 0 & 1 \\\ 0 & 1 & 1 & 1 \\\ \end{matrix} \right\) $

$精确覆盖问题实现$

#include <bits/stdc++.h>
using namespace std;

const int N = 5510;
int n, m;
int row[N], col[N], s[N];
int l[N], r[N], u[N], d[N], idx;
int ans[N], top;

void init()
{
    for (int i = 0; i <= m; i ++ )
    {
        l[i] = i - 1, r[i] = i + 1;
        u[i] = d[i] = i;
    }
    l[0] = m, r[m] = 0;
    idx = m + 1;
}

void add(int& hh, int& tt, int x, int y)
{
    row[idx] = x, col[idx] = y, s[y] ++ ;
    u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
    l[tt] = r[hh] = idx, l[idx] = hh, r[idx] = tt;
    tt = idx ++ ;
}

void remove(int p)
{
    r[l[p]] = r[p], l[r[p]] = l[p];
    for (int i = d[p]; i != p; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
        {
            s[col[j]] -- ;
            u[d[j]] = u[j], d[u[j]] = d[j];
        }       
}

void resume(int p)
{
    r[l[p]] = p, l[r[p]] = p;
    for (int i = d[p]; i != p; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
        {
            u[d[j]] = j, d[u[j]] = j;
            s[col[j]] ++ ;
        }
}

bool dfs()
{
    if (!r[0]) return true;
    int p = r[0];
    for (int i = r[0]; i; i = r[i])
        if (s[i] < s[p])
            p = i;
    remove(p);
    for (int i = d[p]; i != p; i = d[i])
    {
        ans[++ top] = row[i];
        for (int j = r[i]; j != i; j = r[j]) remove(col[j]);
        if (dfs()) return true;
        for (int j = r[i]; j != i; j = r[j]) resume(col[j]);
        top -- ;
    }
    resume(p);
    return false;
}

int main()
{
    scanf("%d%d", &n, &m);
    init();
    for (int i = 1; i <= n; i ++ )
    {
        int hh = idx, tt = idx;
        for (int j = 1; j <= m; j ++ )
        {
            int x;
            scanf("%d", &x);
            if (x) add(hh, tt, i, j);
        }
    }

    if (dfs())
    {
        for (int i = 1; i <= top; i ++ ) printf("%d ", ans[i]);
        puts("");
    }
    else puts("No Solution!");

    return 0;
}

$重复覆盖问题$

同理，由于分枝多，运用$IDA*$优化

$重复覆盖问题实现$

#include <bits/stdc++.h>
using namespace std;

const int N = 110, M = N * N;
int n, m;
int row[M], col[M], s[N];
int l[M], r[M], u[M], d[M], idx;
int ans[N];
bool st[N];

void init()
{
    for (int i = 0; i <= m; i ++ )
    {
        l[i] = i - 1;
        r[i] = i + 1;
        col[i] = u[i] = d[i] = i;
        s[i] = 0;
    }
    l[0] = m, r[m] = 0;
    idx = m + 1;
}

void add(int& hh, int& tt, int x, int y)
{
    row[idx] = x, col[idx] = y, s[y] ++ ;
    u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
    l[tt] = r[hh] = idx, l[idx] = hh, r[idx] = tt;
    tt = idx ++ ;
}

int h()
{
    int cnt = 0;
    memset(st, 0, sizeof st);
    for (int i = r[0]; i; i = r[i])
    {
        if (st[col[i]]) continue;
        cnt ++ ;
        st[col[i]] = true;
        for (int j = d[i]; j != i; j = d[j])
            for (int k = r[j]; k != j; k = r[k])
                st[col[k]] = true;
    }
    return cnt;
}

void remove(int p)
{
    for (int i = d[p]; i != p; i = d[i])
    {
        l[r[i]] = l[i];
        r[l[i]] = r[i];
    }
}

void resume(int p)
{
    for (int i = u[p]; i != p; i = u[i])
    {
        l[r[i]] = i;
        r[l[i]] = i;
    }
}

bool dfs(int k, int depth)
{
    if (k + h() > depth) return false;
    if (!r[0]) return true;

    int p = r[0];
    for (int i = r[0]; i; i = r[i])
        if (s[i] < s[p])
            p = i;

    for (int i = d[p]; i != p; i = d[i])
    {
        ans[k] = row[i];
        remove(i);
        for (int j = r[i]; j != i; j = r[j]) remove(j);
        if (dfs(k + 1, depth)) return true;
        for (int j = l[i]; j != i; j = l[j]) resume(j);
        resume(i);
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &m);
    init();

    for (int i = 1; i <= n; i ++ )
    {
        int hh = idx, tt = idx;
        for (int j = 1; j <= m; j ++ )
        {
            int x;
            scanf("%d", &x);
            if (x) add(hh, tt, i, j);
        }
    }

    int depth = 0;
    while (!dfs(0, depth)) depth ++ ;
    printf("%d\n", depth);
    for (int i = 0; i < depth; i ++ ) printf("%d ", ans[i]);

    return 0;
}