数据结构之线段树

解决问题:

• 区间的某种属性(比如max,min,sum)$O(logn)$

• 单点修改$O(logn)$

• 区间修改

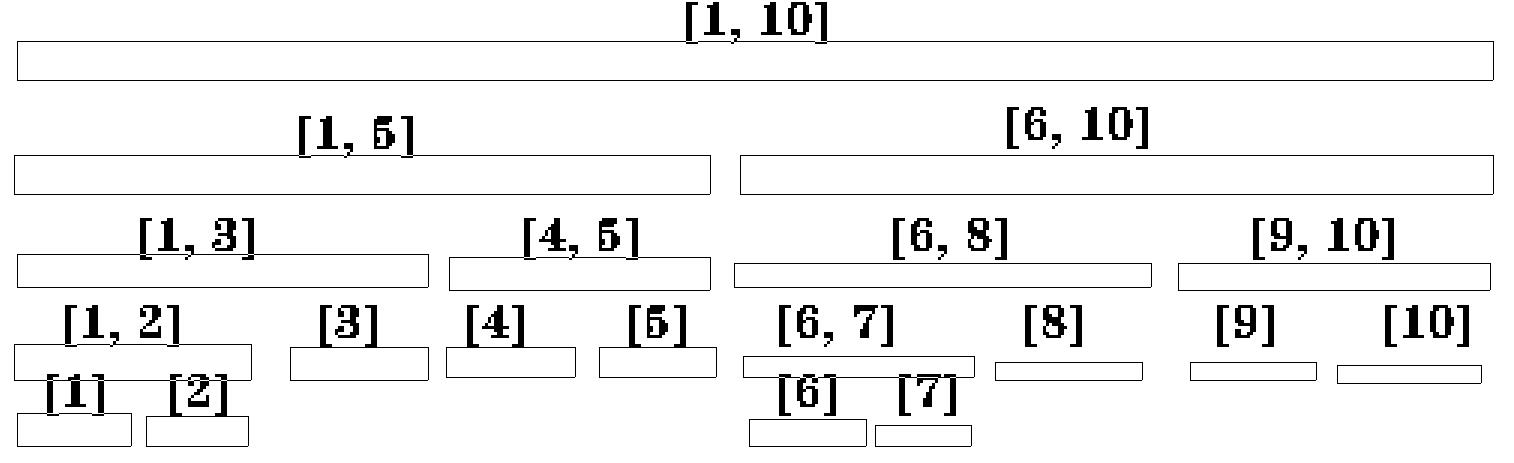
线段树 $ 是每次把一个区间分为两份,直到分成长度为1的若干份为止 $
$ 设有区间[l, r],mid = \frac{l + r}{2} $
$ 那么可以将此区间分为两部分: [l, mid] , [mid + 1, r] $

操作一(初始化build)

$ 初始化函数的作用是初始化出树上每一个节点的左右端点 $
$ 储存格式与堆相同 $
$ 设有一个区间 [l, r] ,编号为 x $

那么 此区间的父节点为 $ \lfloor{\frac{x}{2}} \rfloor $

左儿子为 $ x << 1 $ , 右儿子为 $x << 1 | 1 $

Code

void build(int u, int l, int r){
    tr[u].l = l, tr[u].r = r;//初始化u的值
    //按照题意在此处适当添加信息
    if (l == r)return;
    int mid = l + r >> 1;
    build(u << 1, l, mid),build(u << 1 | 1, mid + 1, r);//分别遍历左右区间
}

操作二(单点修改modify)

$设现在要修改点 x 的值$
$那么从根节点出发走向点x的路径就要跟着修改$
$可以从根节点出发,利用x这个位,一步步深入,最后从下向上更新信息$

Code

void modify_1(int u, int x, int v){
    if (tr[u].l == x && tr[u].r == x) {//如果查找到x,更新这个节点
        tr[u] = {x, x, v, v, v, v};
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid)modify_1(u << 1, x, v);//如果x在左半边,深入左区间
        else modify_1(u << 1 | 1, x, v);//如果x在右半边,深入右区间
        pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);//从下向上更新,用子节点更新父节点
        //根据题意在pushup中适当填入所需信息
    }
}

操作三(区间查询最值query)

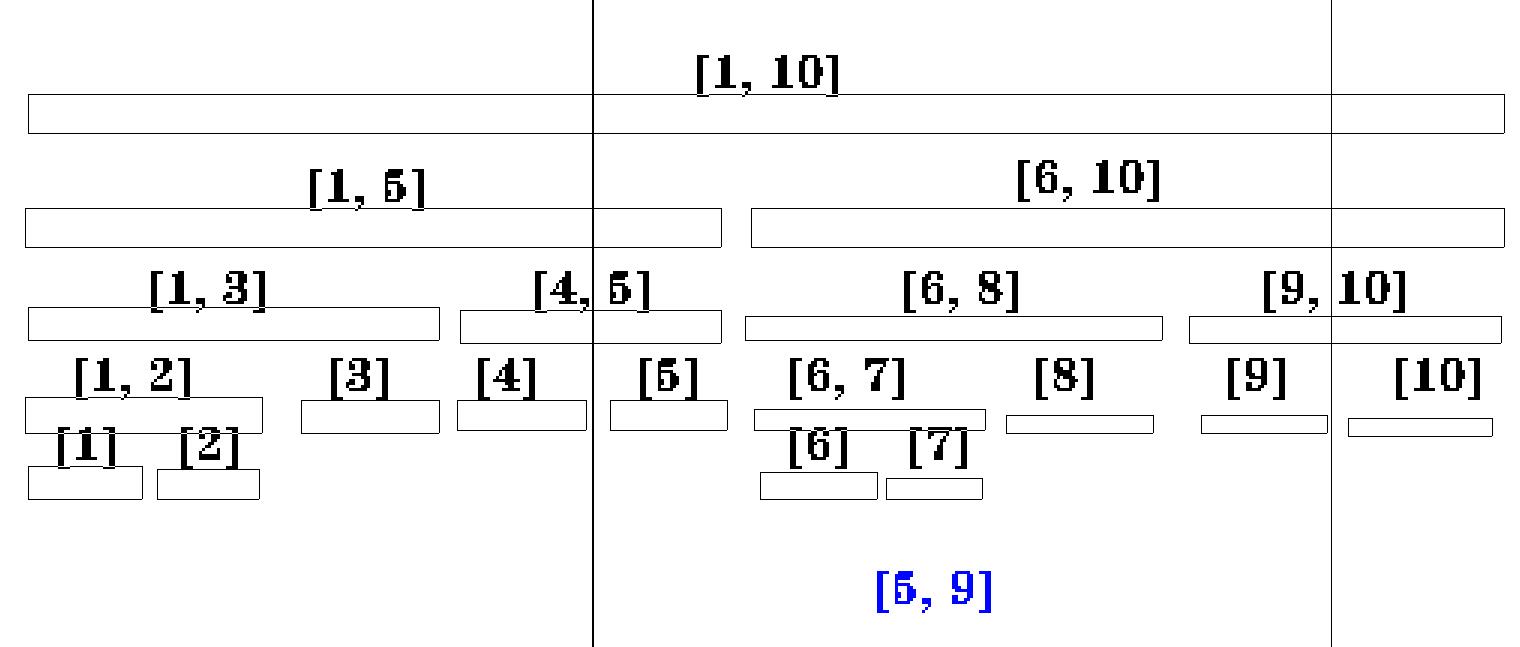
$设现在要求的是区间[l, r]的最大值$
现在所在区间为[Tl, Tr]
分为2种情况:
1. $[Tl, Tr] \in [l, r] ----- 直接返回整个区间,不需要继续递归$
2. $[Tl, Tr] \cap [l, r] \ne \phi ----- 继续向下深入 $

Code

int query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) {
        return tr[u].sum;
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        int tmax = 0;
        if (l <= mid)tmax = max(tmax, query(u << 1, l, r));
        if (r > mid)tmax = max(tmax, query(u << 1 | 1, l, r));
        return tmax;
    }
}

操作四(区间修改pushdown)

$ 当修改操作从单点变成区间时,普通的modify并不能满足题目的要求 $

$ 在解决区间修改的问题是,用到的操作是 $懒标记

$ 使用懒标记时通常在节点信息中添加元素,比如添加 $add$表示节点$u$的所有后代的每一个数都加上$add

$ 懒标记也需要通过遗传的方式传递到叶子节点,及$pushdown函数

Code

void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if (root.add)
    {
        left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

线段树代码模板

#include<bits/stdc++.h>

using namespace std;

const int N = 500010;

int n, m;
int w[N];

struct Node{
    int l, r;
    int sum,add;
}tr[N * 4];

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if (root.add)
    {
        left.add += root.add, left.sum += (left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

void build(int u, int l, int r)
{
    if (l == r)tr[u] = {l, r, w[l], 0};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int l, int r, int d)
{
    if (l <= tr[u].l && tr[u].r <= r)
    {
        tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid)modify(u << 1, l, r, d);
        if (r > mid)modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (l <= tr[u].l && tr[u].r <= r)
        return tr[u].sum;

    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1, res = 0;
    if (l <= mid)res += query(u << 1, l, r);
    if (r > mid)res += query(u << 1 | 1, l, r);

    return res;
}


int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ )
        scanf("%d", &w[i]);

    build(1, 1, n);

    int op, l, r, d;
    while ( m -- )
    {
        scanf("%d%d%d", &op, &l, &r);
        if (op == 1)//修改
        {
            scanf("%lld", &d);
            modify(1, l, r, d);
        }
        else printf("%d\n", query(1, l, r));//查询
    }

    return 0;
}