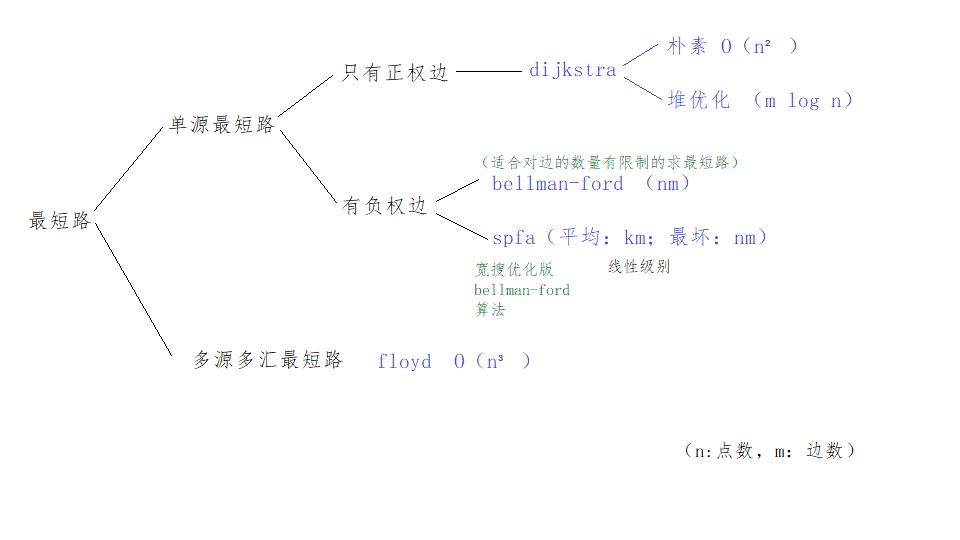
最短路

Dijkstra朴素算法与堆优化算法时间复杂度对比

         稠密图         稀疏图
          m≈n²           m≈n
朴素       n²             n²
堆优化   n² log n       m log n

bellman-ford算法适合：

从起点开始，最多经过k条边，到其他每个点的最短距离。
两重循环：
for(i=0;i<k;i++)//循环边的数量（经过哪些边）
    for(...)//更新每条边

Dijkstra朴素版

①图的存储——邻接矩阵 g[a][b]

②dist[i]:从1号点到i号点的最短路径
算法流程：
初始化：dist[原点]=0,dist[i]=+∞
for(i=0;i<n-1;i++){
    (1)找出剩下点中距离原点最小的点 t
    (2)用t号点更新其他点的距离
}
时间复杂度：O(n²)

无向图->特殊有向图
a——b    a->b
        a<-b

代码如下：

//Dijkstra朴素版 
#include<bits/stdc++.h>
#define N 1000+10
using namespace std;

int n/*点数*/,m /*边数*/;
int g[N][N];//邻接矩阵，存储边 
int dist[N];//存储每条边到原点的距离
bool st[N];//记录当前点是否已被用来更新 

void dijkstra(){
    memset(dist,0x3f,sizeof(dist));//每条边到原点的距离初始化成正无穷
    dist[1]=0;

    for(int i=0;i<n-1;i++){
        //找出剩下点中距离原点最小的点 
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||dist[j]<dist[t]))
                t=j;

        st[t]=true; 
        //从1号点到j号点的距离能否用经过t的一条路径来更新
        //即1->j能否用1->t和t->j路径来更新 
        for(int j=1;j<=n;j++)
            dist[j]=min(dist[j],dist[t]+g[t][j]);
    }
}

int main(){
    cin>>m>>n;

    memset(g,0x3f,sizeof(g));//邻接矩阵初始化 

    while(m--){//存储每条边 
        int a,b,c;
        cin>>a>>b>>c;
        g[a][b]=g[b][a]=min(g[a][b],c);//可能有重边，两点之间只需保留长度最小的边 
    } 

    dijkstra();
    cout<<dist[n];//输出1号点到n号点的最短距离 

    return 0; 
}