题目描述

给定一个长度为 n+1 的数组nums，数组中所有的数均在 1∼n 的范围内，其中 n≥1。

请找出数组中任意一个重复的数，但不能修改输入的数组。

样例
给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。

返回 2 或 3。
思考题：如果只能使用 O(1) 的额外空间，该怎么做呢？

思想：二分 + 分治

抽屉原理：n+1 个苹果放在 n 个抽屉里，那么至少有一个抽屉中会放两个苹果。

抽象解释：

分析：数组长度为n+1 每个元素取值属于[1,n]，则易得至少存在一个重复元素(抽屉原理)

按照【数的取值范围】进行区间划分，每个元素取值都是[1,n] (初始时)将其划分为[1, (1+n)/2] 和 [(1+n)/2 + 1, n] 不妨设 mid = (1 + n) / 2 , 即区间被划分为[1,mid] 和 [mid+1,n]

如此以来则 左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度
反证法：若左右两个区间中的数的个数都小于等于区间长度，则整个区间中数的个数一定小于等于总区间长度，即数组中元素个数 <= n个，显然与n+1个矛盾

根据抽屉原理，得出元素个数比区间长度大区间必定存在重复元素 ——————> 这个新区间不就可以视为和题目开始的求解在整个数组这个大区间中找重复值一样 ————> 迭代这个过程

形象示例：

例：
nums [2 3 5 4 3 2 6 7] n==7
index 0 1 2 3 4 5 6 7

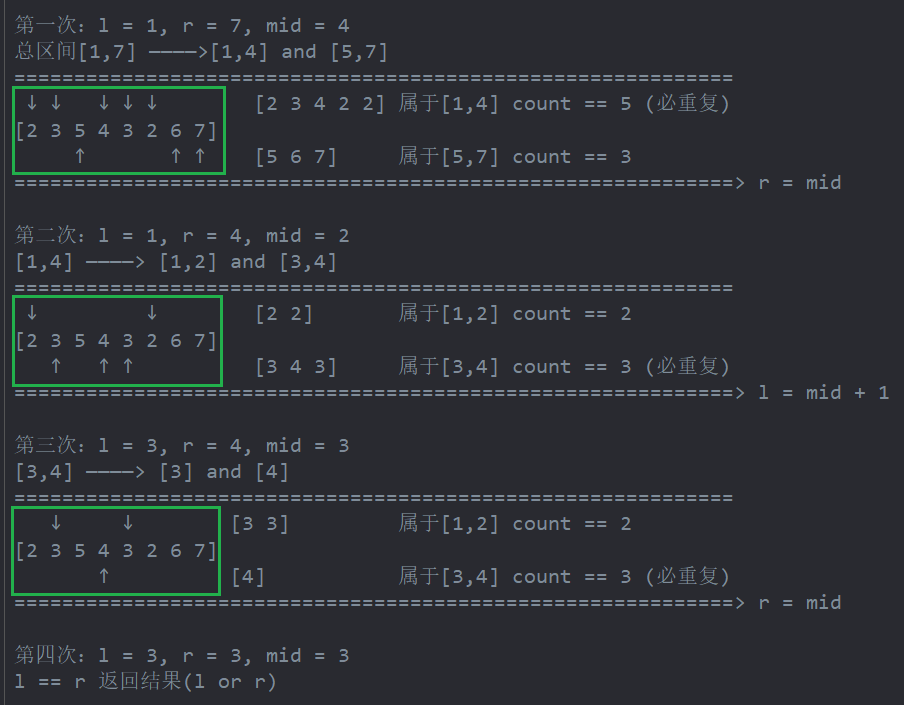
Java代码

class Solution {
    public int duplicateInArray(int[] nums) {
        //抽屉原理 + 分治
        //数组长度为n + 1, 数组中所有的数均在 1∼n 的范围,则必然至少存在一个重复元素
        int l = 1, r = nums.length - 1; // [l,r] == [1,n] 按数值划分区间（与索引无关）

        //将区间划分 [l,mid] 和 [mid+1,r] >>按数值<< 划分区间（与索引无关）
        while (l < r) {
            int count = 0;
            int mid = l + r >> 1;
            for (int x : nums) {
                count += (l <= x && x <= mid ? 1 : 0); //记录数值在[l,mid]区间内的元素个数
            }
            if (count > (mid - l + 1)) { //上面统计的个数如果大于这个区间长度,则这个[l,mid]区间必定有重复元素
                r = mid ; //向l侧缩小查找区间
            } else {
                l = mid + 1; //向r侧缩小查找区间
            }
        }

        return l; //l == r
    }
}