引理

若M个小朋友排成一行，手中分别有A[1]~A[n]个糖果，在每一步操作中，可以让某个人把自己手中的一个糖果交给他旁边的一个人，求至少需要多少步操作才能让每个小朋友手中的糖果数相等？

分析：

• 在第一个人中，一定会向第二个人拿糖果或者向第二个人给糖果，其数量为|A[1] - avg|,更新A[2]

• 在第二个人中，一定会向第三个人拿糖果或者向第三个人给糖果，其数量为|A[2] - avg|,更新A[3]

• …

• 在第(n - 1)个人中，一定会向第n个人拿糖果或者向第n个人给糖果，其数量为|A[n - 1] - avg|,更新A[n]

即使在某个时刻有某个A[i]被减为负数也没关系，因为接下来A[i]会从A[i + 1]处拿

步骤

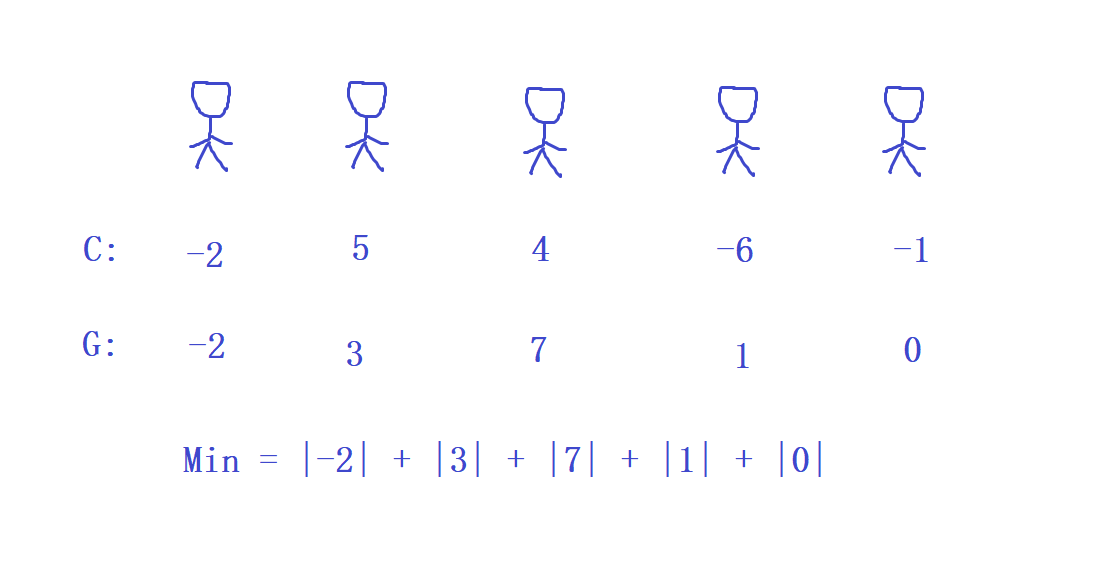
• 1、求出每个糖果数-糖果平均数avg的值作为数组C[],则C[i] = A[i] - avg,其中i∈ [1,n]

• 2、求出数组C[]的前缀和S[],则达到目标所需要的最小步数是$$ Min = \sum_{i=1}^n\| G[i] | $$

算法1

.....此处是一个环形的糖果交换问题，则一定存在一种最优解使得某两个人之间没有纸牌交换。就是要么a给b，要么b给a，不能a给了b，b又给了a，如果存在这样的交换，就不是最优解了，可以用反证法证明。

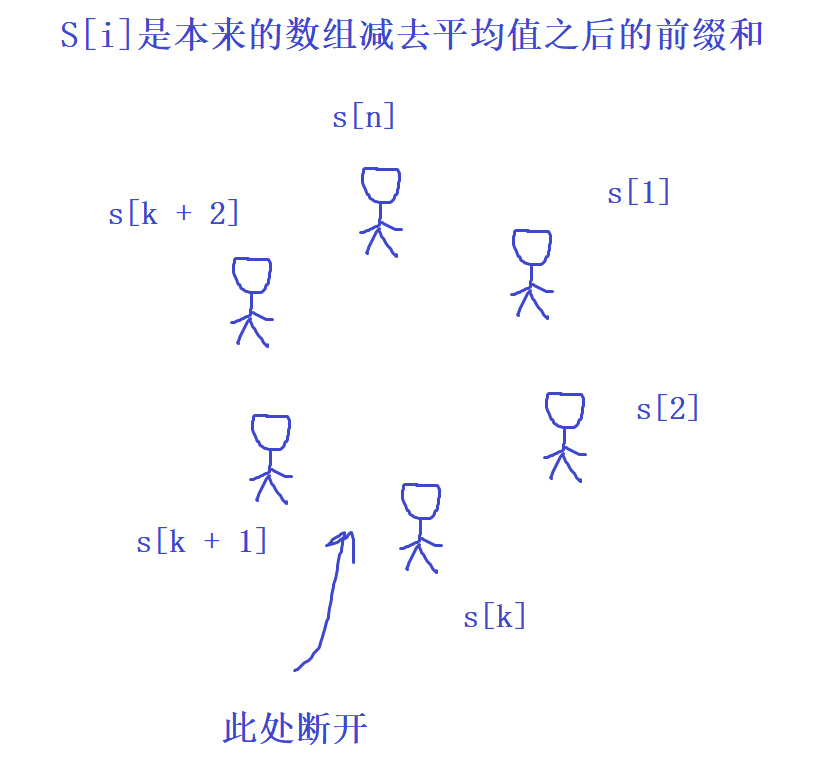
不妨设S[i]是本来的数组减去平均值之后的前缀和，假设我们从第k个位置断开（严格的来说是第k个位置的下一条边断开）,那么序列就变成了：

• A[k + 1] = S[k + 1] - S[k]

• A[k + 2] = S[k + 2] - S[k]
  …
  A[n] = s[n] - s[k]
  A[1] = S[1] + S[n] - S[k]

• …

• A[k] = S[k] + S[n] - S[k]

• 断开之后则可以看成是排成一行，引用上面的引理
  则相当于求|S[k + 1] - S[k]| + |S[k + 2] - S[k]| + … + |S[n] - S[k]| + |S[n] - S[k] + S[1]| + |S[n] - S[k] + S[2]| +…+|S[n] - S[k] + S[k]|的最小值，由于S[n] = 0
  则相当于求|S[1] - S[k]| + |S[2] - S[k]| +…+ |S[k] - S[k]| + |S[k + 1] - S[k]| +…+ |S[n] - S[k]| 的最小值，其中k∈ [1,n]
  

则此问题变成了货仓选址问题，找到中位数，累加出每个点到中位数的距离之和，链接如下

https://www.acwing.com/file_system/file/content/whole/index/content/132044/

步骤

• 1、计算出本来数组减去平均值之后的前缀和s[]

• 2、对数组s[]进行排序

• 3、累加出每个点到中位数的距离之和res += Math.abs(s[i] - s[(n + 1)/2])

时间复杂度 $O(nlogn)$

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int[] s = new int[1000010];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        long sum = 0;
        for(int i = 1;i <= n;i++) 
        {
            s[i] = scan.nextInt();  
            sum += s[i];
        }
        //求平均值
        int avg = (int) (sum/n);
        //求减去平均值之后的数组的前缀和
        for(int i = 1;i <= n;i++)
        {
            s[i] = s[i] - avg + s[i - 1];
        }
        Arrays.sort(s, 1, n + 1);
        long res = 0;
        for(int i = 1;i <= n;i++) res += Math.abs(s[i] - s[(n + 1)/2]);
        System.out.println(res);
    }
}

算法2

步骤

• 1、计算出本来数组减去平均值之后的前缀和s[]

• 2、通过找第k小的方式找出中位数，其中这里的时间复杂度是O(n)

• 3、累加出每个点到中位数的距离之和res += Math.abs(s[i] - s[k])

注意：找第k小的数，我们只需要进入左右两半二者之一继续递归，在平均情况下，复杂度为n + n/2 + n/4 +... + 1 = O(n)

时间复杂度 $O(n)$

Java 代码

import java.util.Arrays;
    import java.util.Scanner;

    public class Main {
        //找第k个位置 时间复杂度O(n)
        public static int quick_sort(int[] q,int L,int R,int k)
        {
            if(L >= R) return L;
            int i = L - 1;
            int j = R + 1;
            int x = q[(L + R) >> 1];
            while(i < j)
            {
                do i++; while(q[i] < x);
                do j--; while(q[j] > x);
                if(i < j) 
                {
                    int t = q[i];
                    q[i] = q[j];
                    q[j] = t;
                }
            }
            //j是左边界
            if(k <= j) return quick_sort(q,L,j,k);
            else return quick_sort(q,j + 1,R,k);
        }
        static int[] s = new int[1000010];
        public static void main(String[] args) {
            Scanner scan = new Scanner(System.in);
            int n = scan.nextInt();
            long sum = 0;
            for(int i = 1;i <= n;i++) 
            {
                s[i] = scan.nextInt();  
                sum += s[i];
            }
            //求平均值
            int avg = (int) (sum/n);
            //求减去平均值之后的数组的前缀和
            for(int i = 1;i <= n;i++)
            {
                s[i] = s[i] - avg + s[i - 1];
            }
            int k = quick_sort(s,1,n,(n + 1) >> 1);

            long res = 0;
            for(int i = 1;i <= n;i++) res += Math.abs(s[i] - s[k]);
            System.out.println(res);
        }
    }