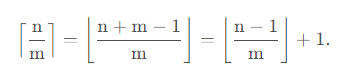广义鸽巢原理： 把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体。
错误证明：
假设不存在抽屉中至多有（m-1）个物体
即所有抽屉，每个抽屉物体数都大于m-1
那么物体总数大于mn-n
被卡住
因为这样推不出矛盾
改成如下证明：
假设不存在抽屉中至多有（m—1）个物体
即所有抽屉，每个抽屉物体数都大于m-1，即大于等于m
那么物体总数大于等于mn
推出了矛盾
由此可见离散数学中由个体满足的性质拓展到整体时，x>=y和x>y-1不能当作等价的v条件
因为两边乘以倍数后容易放缩过度，而转换为含有大（小）于等于的式子放缩更精密，不容易放缩过度

上面问题是学习P180.排书的上下取整恒等式时发现的
参考链接，留待日后学习
先记住结论：