题目链接
A

统计每次ab的积分，如果(a > b + y) || (b > a + x)那么另一方无胜算
如果最后还没有分出胜负，cout-1

#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
char s[15];
void solve()
{
    scanf("%s", s+1);
    int a = 0, b = 0;//得分情况
    int x = 5, y = 5;//还剩几场
    for (int i = 1; i <= 10; i++)
    {
        if (i % 2)//奇数
        {
            if (s[i] == '1')
                a++;
            x--;
        }
        else
        {
            if (s[i] == '1')
                b++;
            y--;
        }
        if ((a > b + y) || (b > a + x))
        {
            cout << i << endl;
            return;
        }
    }
    cout << -1 << endl;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

L

数学题，数学期望

答案：32

C

诈骗题，规律

#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;
int a[N], h[N], maxx;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        maxx = 0;
        int cnt = 1;
        memset(h, 0, sizeof h);
        int n, num = 1;
        cin >> n;
        for (int i = 1; i <= n; i++)
        {
            cin>>a[i];
            if(a[i]>0)maxx++;
        }
        cout << maxx << endl;
    }
    return 0;
}

H

诈骗，根本不用关心拼图缺少的部分

//不变0，里1，外2
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        int que = 0;
        int sum = n * n * 10;
        for (int i = 1; i <= n * n - 1; i++)
        {
            string a;
            cin >> a;
            for (int i = 0; i < a.size(); i++)
            {
                if (a[i] == '1')que += 1;
                if (a[i] == '2')que -= 1;
            }
        }
        cout << 10 + que << endl;
    }
    return 0;
}

D

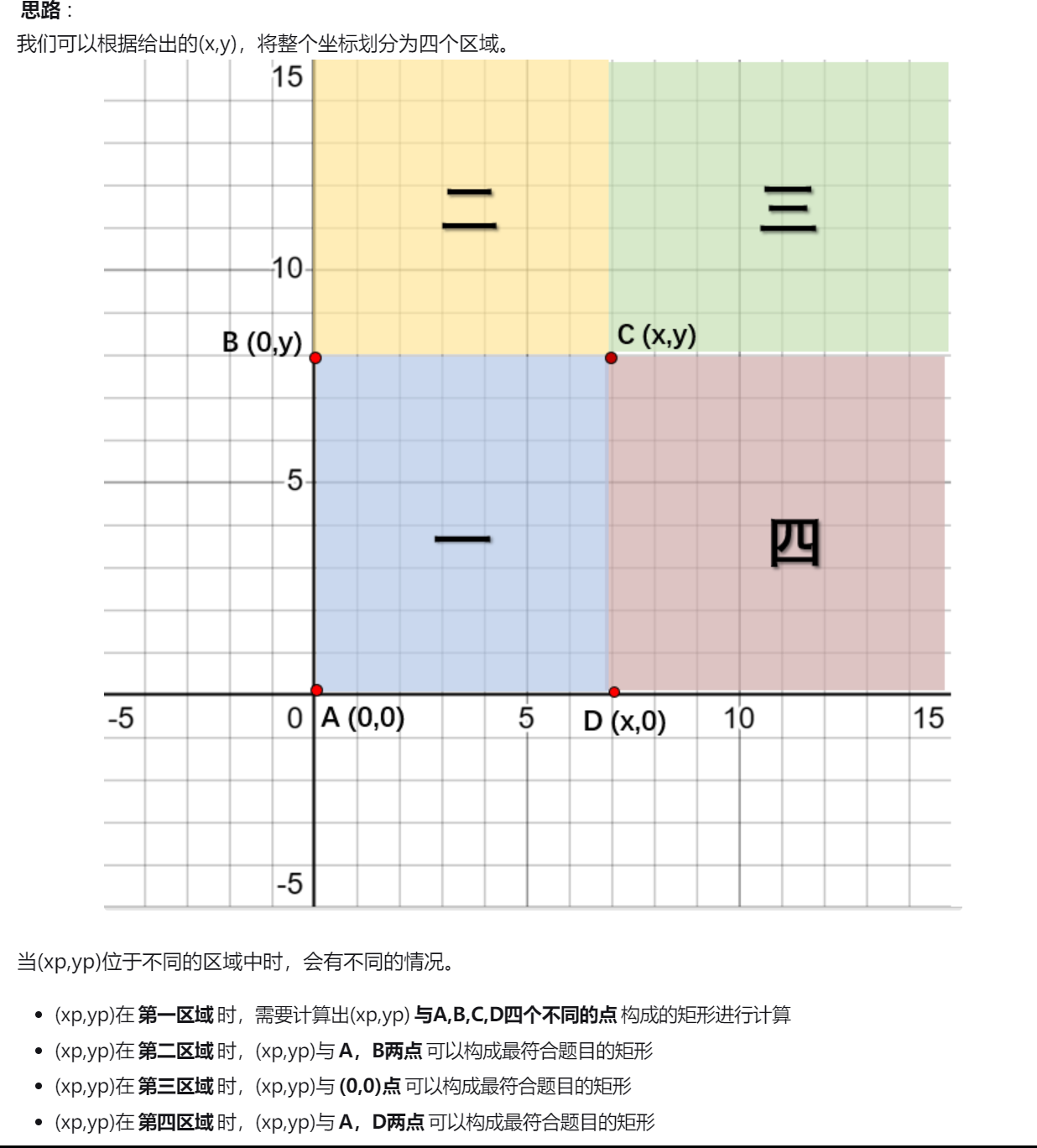
数学
分四个界限
（交集的面积）/（并集的面积）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll x, y, xp, yp;
void solve()
{
    scanf("%lld%lld%lld%lld", &x, &y, &xp, &yp);
    double res = 0;

    if (xp <= x && yp <= y) // 在第一区域
    {
        res = max(xp * yp / (double)(x * y), // (xp,yp)与 A(0,0) 构成的矩形
            xp * (y - yp) / (double)(x * y)); // (xp,yp)与 D(0,y) 构成的矩形

        res = max(res, (x - xp) * yp / (double)(x * y));// (xp,yp)与 B(x,0) 构成的矩形

        res = max(res, (x - xp) * (y - yp) / double(x * y));// (xp,yp)与 C(x,y) 构成的矩形

        printf("%.10f\n", res);
        return;
    }

    if (xp <= x) // 在第二区域
    {
        res = max(xp * y / (double)(x * y + xp * (yp - y)), // (xp,yp)与 A(0,0) 构成的矩形
            (x - xp) * y / (double)(x * y + (x - xp) * (yp - y)));// (xp,yp)与 B(x,0) 构成的矩形
        printf("%.10f\n", res);

        return;
    }
    if (yp <= y) // 第四区域
    {
        res = max(x * yp / (double)(x * y + yp * (xp - x)), // (xp,yp)与 A(0,0) 构成的矩形
            x * (y - yp) / (double)(x * y + (y - yp) * (xp - x)));// (xp,yp)与 D(0,y) 构成的矩形
        printf("%.10f\n", res);
        return;
    }
    // 第三区域
    res = x * y / (double)(xp * yp); // (xp,yp)与 A(0,0) 构成的矩形
    printf("%.10f\n", res);
}
int main()
{
    int T;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

K

贪心，枚举，最小值，dp；
1.贪心做法：先把100摆好剩下111，这样的情况最少了
2.dp做法（不会）

#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
int n,m;
int main()
{
    cin>>n>>m;
    int t=n-m;//0
    vector<int>s;
    while(m||t)
    {
        if(m)s.push_back(1),m--;
        if(t)s.push_back(0),t--;
        if(t)s.push_back(0),t--;
    }
    int ans=0;
    for(int i=1;i<n-1;i++)
    {
        if(s[i]+s[i-1]+s[i+1]>=2)
        ans++;
    }
    cout<<ans<<endl;
    return 0;
}

M(DP)

状态划分：枚举到第i个人的仙贝k，由i-1状态延续，分出去的共j个，k是当前i收到的仙贝数量
初始dp[0][0]=0;答案枚举到dp[n][m];
dp[i][j]=(k<=j)max(dp[i-1][j-k]+k/(m-(j-k)))
【m-(j-k)】剩下的仙贝数量

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int>PII;
typedef double db;
int n, m;
db dp[510][510];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= j; k++)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k] + (db)k / (m - (j - k)));
    db ans = 0;
    for (int i = 0; i <= n; i++) 
        for (int j = 0; j <= m; j++) 
            ans = max(ans, dp[i][j]);
    printf("%.9lf\n", ans);
    return 0;
}

G

经多次操作收敛到一个不变的值
数学，x有三个值0，99，100（打表发现最多20次值不再改变）：
跑f(x)=round(10*sqrt(x))发现，0无论跑多少次都是0，
[1,99]跑有限次就达到99不再变化，[100,∞]也是跑有限次达到100后就不再变化，
所以只需要存储下来非0的下标，以及多少次操作后就不再变化的操作数
，操作时只修改还会变化的，否则从数组中删去，并修改所有数的和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int, int>pii;
ll n, m, a[100010], ans;
int op, l, r, k;
set<int>st;
int f(int x)
{
    return round(sqrt(x) * 10);//round四舍五入函数
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        ans += a[i];
        if (f(a[i]) != a[i])
        {
            st.insert(i);
        }
    }
    st.insert(n + 1);//方便退出循环
    for (int i = 1; i <= m; i++)
    {
        scanf("%d", &op);
        if (op == 1)
        {
            scanf("%d%d%d", &l, &r, &k);
            int pos = l;
            while (1)
            {
                int nxt = (*st.lower_bound(pos));
                if (nxt > r)break;
                for (int t = 1; t <= min(k,20); t++)
                {
                    ans -= a[nxt];
                    a[nxt] = f(a[nxt]);
                    ans += a[nxt];
                }
                if (f(a[nxt]) == a[nxt])st.erase(nxt);
                pos = nxt + 1;
            }
        }
        else
        {
            printf("%lld\n", ans);
        }
    }
    return 0;
}

F

还不太理解

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int p[N], cnt, S[N];
bool st[N];
int find(int x)
{
    if (x != p[x])
        p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n, m, a, b;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
        p[i] = i, S[i] = 1;
    while (m -- )
    {
        cin >> a >> b;
        a = find(a), b = find(b);
        if (a == b) continue;
        S[b] += S[a];
        p[a] = b;
    }
    LL res = 0, ans = 0;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> a;
        if (a)
        {
            int pa = find(i);
            if (!st[pa])
                ans += 1ll * S[pa] *S[pa], st[pa] = true, cnt ++;
        }
        if (i == find(i)) res += 1ll * S[i] * S[i];
    }
    if (!cnt) cout << res << endl;
    else if (cnt == 1) cout << ans << endl;
    else cout << 0 << endl;
    return 0;
}

E（大佬的题解）

叉乘：（注意精度）
上面向量BA（ax-bx,ay-by）与向量BC（cx-bx,cy-by）的叉乘为

　　　　　　 BA*BC= (ax-bx)*(cy-by)-(ay-by)*(cx-bx);

　　　　　　根据右手法则，其方向，垂直屏幕向里

　　　　　　向量 EF与向量ED同理，但是方向是垂直屏幕向外

　　　　　　两者的值算出来最后是一正一负

　　　　　　可以分辨出来

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const double esp = 1e-5;
double get(double x1, double y1, double x2, double y2)
{
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
double cross(double xz, double yz, double xl, double yl, double xs, double ys)
{
    // 长的边的向量：
    double ux = xl - xz, uy = yl - yz;
    // 短的边的向量：
    double vx = xs - xz, vy = ys - yz;
    return ux * vy - uy * vx;
}
void solve()
{
    double xa, ya, xb, yb, xc, yc, xd, yd, xe, ye, xf, yf;
    cin >> xa >> ya >> xb >> yb >> xc >> yc;
    cin >> xd >> yd >> xe >> ye >> xf >> yf;
    double BA = get(xb, yb, xa, ya), BC = get(xb, yb, xc, yc);
    double du1, du2;
    if (abs(BA - BC) < esp)
    {
        cout << "NO" << endl;
        return;
    }
    else if (BA > BC)
        du1 = cross(xb, yb, xa, ya, xc, yc);
    else
        du1 = cross(xb, yb, xc, yc, xa, ya);
    double ED = get(xe, ye, xd, yd), EF = get(xe, ye, xf, yf);
    if (ED > EF)
        du2 = cross(xe, ye, xd, yd, xf, yf);
    else if (ED < EF)
        du2 = cross(xe, ye, xf, yf, xd, yd);
    if (du1 * du2 < 0)
        cout << "YES" << endl;
    else
        cout << "NO" << endl;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

I（暂时没理解完）

不可能有两个及以上的牛牛点

#include <bits/stdc++.h>

# define IO ios::sync_with_stdio(false);
# define Icin cin.tie(nullptr);cout.tie(nullptr);
# define int long long
# define fi first
# define se second
# define endl "\n"
# define pb push_back
# define rep(i,a,b) for(int i=a;i<=b;i++)

using namespace std;

typedef long double ld;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<long long, long long> PII;
typedef pair<ld, ld> PDD;
typedef pair<int, string> PIS;
typedef pair<ld, int> PDI;

const int N = 1e6 + 10;
const ld eps = 1e-5;

const int inf = 0x3f3f3f3f, mod = 998244353;


int n, m;
map<int, int> mp, mp2;
set<int> st;
deque<int> q;
vector<int> v[N];
int a[110][110];
int f[10010];
int dx , dy , cnt;


void puts0()
{
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= n ; j ++ )
            cout << "0 ";
        cout<<endl;
    }
}

bool check()
{
    int mx = 0 , mn = inf;


    //行最大
    for(int i = 1 ; i <= n ; i ++ )
    {
        if(i == dy) continue;

        if(!a[dx][i])
        {
            while(!q.empty() && f[q.front()]) q.pop_front();
            a[dx][i] = q.front();
            q.pop_front();
            f[a[dx][i]] = 1;
        }
        mx = max(mx, a[dx][i]);
    }
    //列最小
    for(int i = 1 ; i <= n ; i ++ )
    {
        if(i == dx) continue;

        if(!a[i][dy])
        {
            while(!q.empty() && f[q.back()]) q.pop_back();
            a[i][dy] = q.back();
            q.pop_back();
            f[a[i][dy]] = 1;
        }
        mn = min(mn, a[i][dy]);
    }
//  cout<<mx<<" "<<mn<<endl;
    //还没填过，就在行最大，列最小范围内看有没有符合的
    if(!a[dx][dy])
    {
        for(int i = mx + 1 ; i < mn ; i ++ )
        {
            if(!f[i])
            {
                a[dx][dy] = i;
                f[i] = 1;
                break;
            }
        }
    }

    //还是0
    //或者值不符合范围
    if(!a[dx][dy]) return false;
    if(a[dx][dy] < mx || a[dx][dy] > mn) return false;

    return true;

}


void sv()
{
    //没用过的放进来
    for(int i = 1 ; i <= n * n ; i ++ )
    {
        if(!f[i]) q.push_back(i);
    }

    //如果有一个牛牛点
    if(cnt == 1)
    {
        //不能放
        if(!check())
        {
            puts0();
            return ;
        }
    }
    //可以就继续

    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= n ; j ++ )
        {
            if(!a[i][j])
            {
                while(!q.empty() && f[q.front()]) q.pop_front();
                a[i][j] = q.front();
                q.pop_front();
            }

            cout << a[i][j] << " ";
        }
        cout << endl;
    }
}


void solve() {

    //初始化
    memset(a , 0 , sizeof a);
    memset(f , 0 , sizeof f);
    while(!q.empty()) q.pop_back();
    cnt = 0;


    cin >> n >> m ;

    int op, x, y, z;

    while(m -- )
    {
        cin >> op >> x >> y;
        if(op == 1)
        {
            cin >> z;
            a[x][y] = z;
            f[z] = 1;
        }
        else{
            dx = x , dy = y;
            cnt ++;
        }
    }
    //超过一个不可能的
    if(cnt > 1)
    {
        puts0();
        return;
    }

    sv();
}



signed main() {
    IO;
    Icin;
    //cout<<endl;

    int t = 1;
    cin >> t;

    //cout << fixed;
    cout << fixed << setprecision(9);

    while (t--) {
        solve();
    }

    return 0;
}