树与图的存储
树是一种特殊的图,与图的存储方式相同。
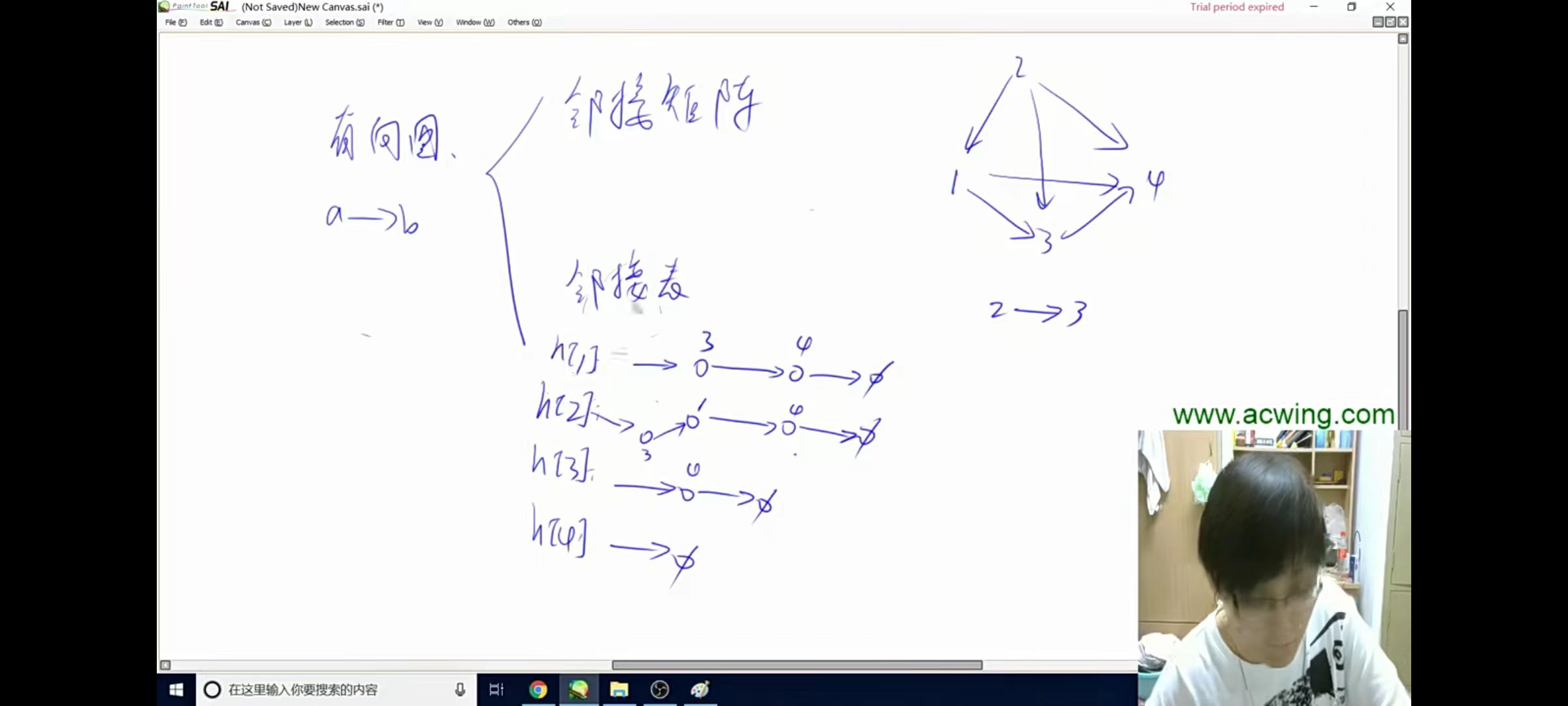
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
(2) 邻接表:
和哈希表的拉链法类似。
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;
// 添加一条边a->b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);
树与图的遍历
时间复杂度 O(n+m)O(n+m), nn 表示点数,mm 表示边数
(1) 深度优先遍历 —— 模板题 AcWing 846. 树的重心
int dfs(int u)
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}
(2) 宽度优先遍历 —— 模板题 AcWing 847. 图中点的层次
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
题目描述
给定一颗树,树中包含n个结点(编号1~n)和n-1条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数n,表示树的结点数。
接下来n-1行,每行包含两个整数a和b,表示点a和点b之前存在一条边。
输出格式
输出一个整数m,表示重心的所有的子树中最大的子树的结点数目。
数据范围
1≤n≤105
样例
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4
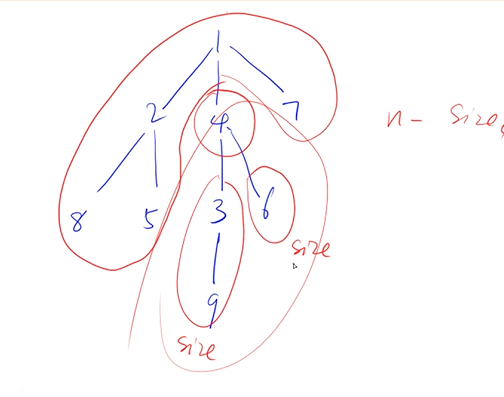
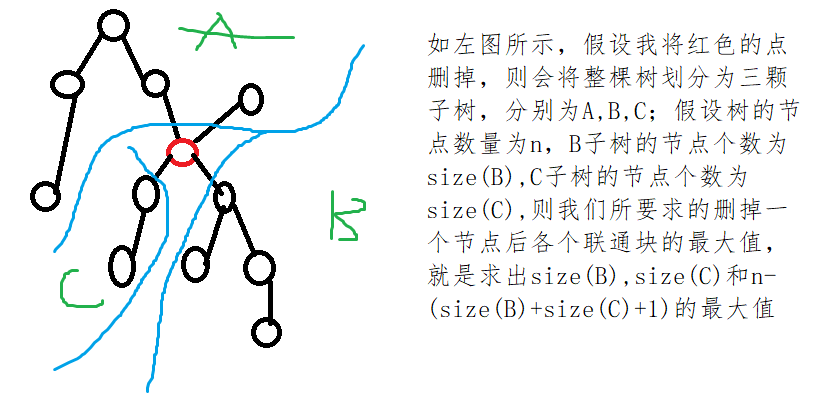
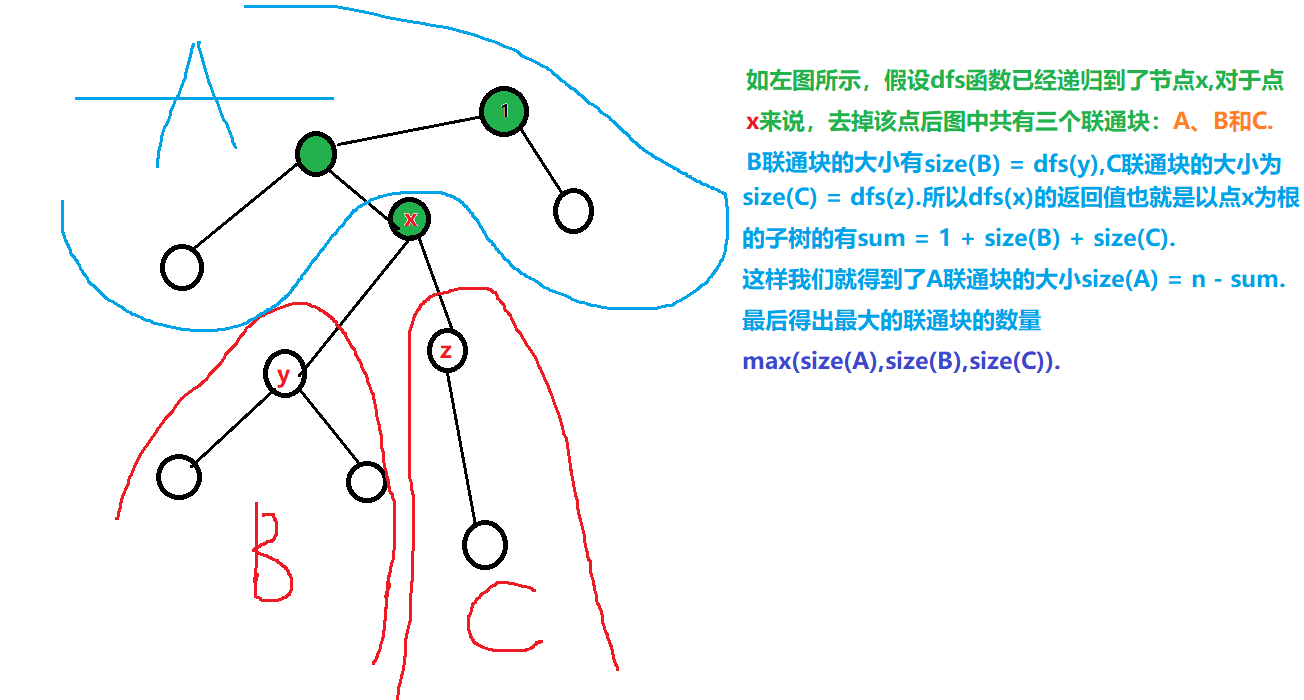
结论
在本题的邻接表存储结构中,有两个容易混淆的地方,一个是节点的编号,一个是节点的下标。
节点的编号是指上图所画的树中节点的值,范围是从1~n。在本题中,每次输入的a和b就是节点的编号,编号用e[i]数组存储。
节点的下标指节点在数组中的位置索引,数组之间的关系就是通过下标来建立连接,下标用idx来记录。idx范围从0开始,如果idx==-1表示空。
1:->4->7->2
2:->5->8->1
e[i]的值是编号,是下标为i节点的编号,如例1:e[0]=4,e[1]=7,e[2]=2。
ne[i]的值是下标,是下标为i的节点的next节点的下标,e[0]=2,e[1]=3;e[3]=-1。
h[i]存储的是下标,是编号为i的节点的next节点的下标,比如编号为1的节点的下一个节点是4,那么我输出e[h[1]]就是4h[1]=0,e[h[1]]=4;
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图,所以每个节点至多对应2n-2条边
int h[N]; //邻接表存储树,有n个节点,所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入,n个节点
int ans = N; //表示重心的所有的子树中,最大的子树的结点数目
bool st[N]; //记录节点是否被访问过,访问过则标记为true
//a所对应的单链表中插入b a作为根
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;//插在头节点,a为根可以到的点,最前面,不同于链表比较方便
}
// dfs 框架
/*
void dfs(int u){
st[u]=true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
*/
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u) {
int res = 0; //存储 删掉某个节点之后,最大的连通子图节点数
st[u] = true; //标记访问过u节点
int sum = 1; //存储 以u为根的树 的节点数, 包括u,如图中的4号节点
//访问u的每个子节点
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];//用e[i]来存储节点的数值,取出来
if (!st[j]) {//因为每个节点的编号都是不一样的,所以 用编号为下标 来标记是否被访问过
int s = dfs(j); // u节点的单棵子树节点数 如图中的size值
res = max(res, s); // 记录最大联通子图的节点数,就是取出u以后两个的最大值
sum += s; //以j为根的树 的节点数
}
}
//n-sum 如图中的n-size值,不包括根节点;
res = max(res, n - sum); // 选择u节点为重心,最大的 连通子图节点数
ans = min(res, ans); //遍历过的假设重心中,最小的最大联通子图的 节点数
return sum;//返回以u为根的子树中节点的个数,包括u。
}
int main() {
memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
cin >> n; //表示树的结点数
// 题目接下来会输入,n-1行数据,
for (int i = 0; i < n - 1; i++) { // 树中是不存在环的,对于有n个节点的树,必定是n-1条边
int a, b;
cin >> a >> b;
add(a, b), add(b, a); //无向图
}
dfs(1); //可以任意选定一个节点开始 u<=n。选择的节点,不是位置
cout << ans << endl;
return 0;
}
树与图的广度优先遍历
2) 宽度优先遍历 —— 模板题 AcWing 847. 图中点的层次
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
题目描述(图中点的层次)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤105
输入样例
4 5
1 2
2 3
3 4
1 3
1 4
输出样例
1
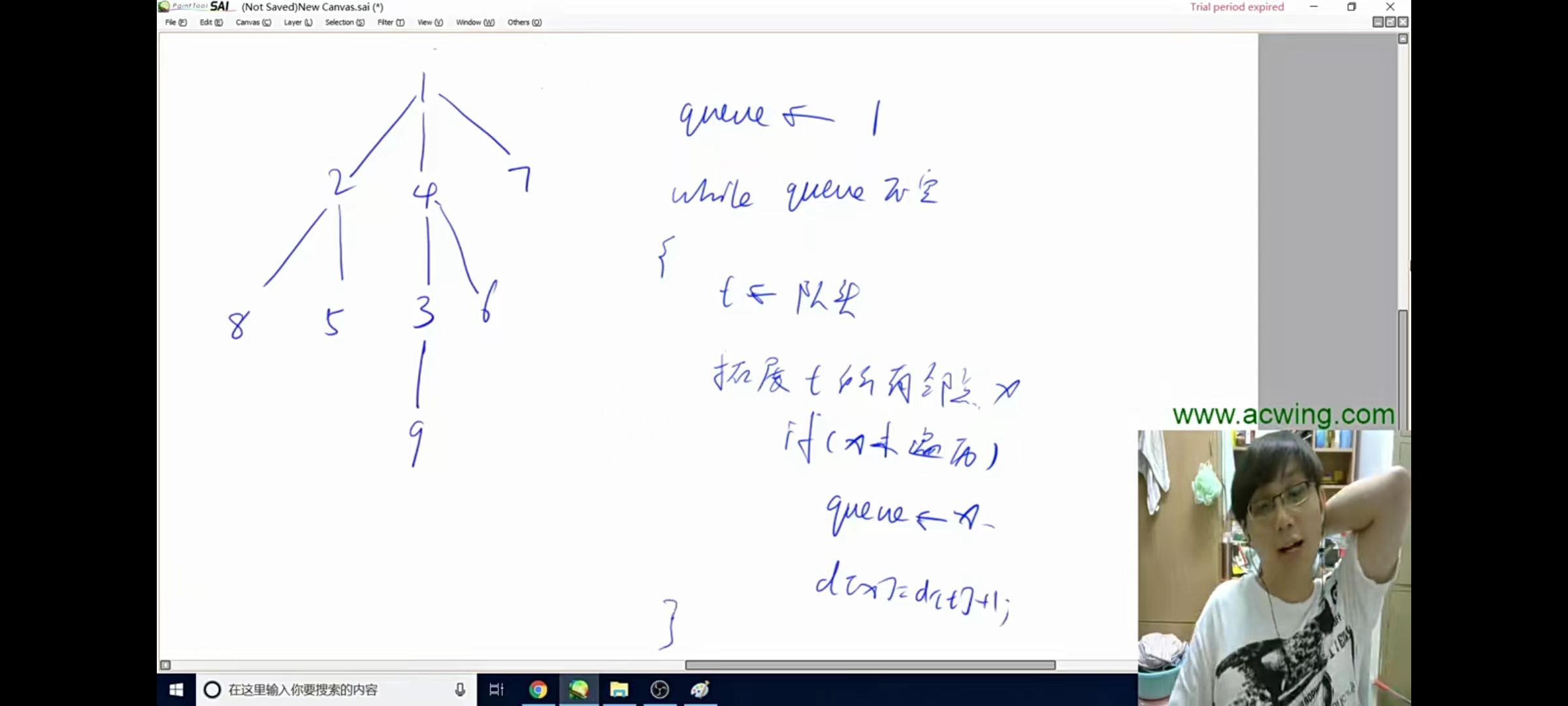
1.模拟数组
#include <cstring>
#include <iostream>
using namespace std;
const int N=1e5+10;
int h[N], e[N], idx, ne[N];
int d[N]; //存储每个节点离起点的距离 d[1]=0
int n, m; //n个节点m条边
int q[N]; //存储层次遍历序列 0号节点是编号为1的节点
void add(int a, int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
int hh=0,tt=0;
q[0]=1; //0号节点是编号为1的节点,可以换点,是拉链法换对头
memset(d,-1,sizeof d);//先初始化,在赋值d[n]=0;要不然少一。
d[1]=0; //存储每个节点离起点的距离 从1号节点开始,距离为0,从2开始,d[2]=0
//当我们的队列不为空时
while(hh<=tt)
{
//取出队列头部节点
int t=q[hh++];
//遍历t节点的每一个邻边
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
//如果j没有被扩展过
if(d[j]==-1)
{
d[j]=d[t]+1; //d[j]存储j节点离起点的距离,并标记为访问过
q[++tt] = j; //把j结点 压入队列
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
cout<<bfs()<<endl;
}
2.stl
#include<iostream>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],e[N],ne[N],idx;
int d[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
memset(d,-1,sizeof d);宽搜模板,如果换点就换对头,d[x]=0,也改变
queue<int> q;
d[1]=0;
q.push(1);
while(q.size())
{
int t=q.front();
q.pop();
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]==-1)
{
d[j]=d[t]+1;
q.push(j);
}
}
}
return d[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
}
printf("%d ",bfs());
return 0;
}
2.模板
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int e[N],ne[N],h[N],d[N],idx;
int m,n;
bool st[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs()
{
queue<int>q;
q.push(1);
st[1]=true;
memset(d,-1,sizeof d);
d[1]=0;
while(q.size())
{
int t=q.front();
q.pop();
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
d[j]=d[t]+1;
st[j]=true;
q.push(j);
}
}
}
return d[m];
}
int main()
{
cin>>m>>n;
memset(h,-1,sizeof h);
while(n--)
{
int a,b;
cin>>a>>b;
add(a,b);
}
printf("%d",dfs());
return 0;
}
