前缀和与差分。
一、前缀和与差分的关系
互为逆运算。
1、设前缀和数组为s,原数组为a
则s是a的前缀和数组,a为s的差分数组
前缀和与差分互为逆运算。——yxc
二、前缀和
1、一维前缀和的基本原理
请看题目: ACWING.795前缀和
本题要求给定数组返回数组l-r之间所有数的和。
如果用朴素算法那时间复杂度可能会高到超时!
如果用朴素算法那时间复杂度可能会高到超时!
如果用朴素算法那时间复杂度可能会高到超时!重要是事情说三遍。
所以,我们采用大部分算法的思路:初始化(后面KMP也是这样)
先初始化一个s数组,s[i] = s[i - 1] + a[i];
换成人话说就是s[i]表示a[0]-a[i]所有数的和。
然后针对每个询问进行查找即可。
模板:
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> a[i];
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
while (m -- )
{
int l, r;
cin >> l >> r;
cout << s[r] - s[l - 1] << endl;//请看y总视频
}
return 0;
}
天梯爱好者可以采用以下快速模板,能把时间减少至40秒以内。(我真能水,自己最高39s)
#include<iostream>
using namespace std;
const int N = 100010;
int n,m,a[N],s[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]=s[i-1]+a[i];
}
while(m--)
{
int l,r;cin>>l>>r;
cout<<s[r]-s[l-1]<<endl;
}
}
二维前缀和的基本原理。
二维前缀和相比于一维更难(废话)
请看题目: ACWING.796子矩阵的和
本题要求给定一个矩阵,求指定范围的面积。
本题为二维前缀和,用到容斥原理的思路。
请看此图:
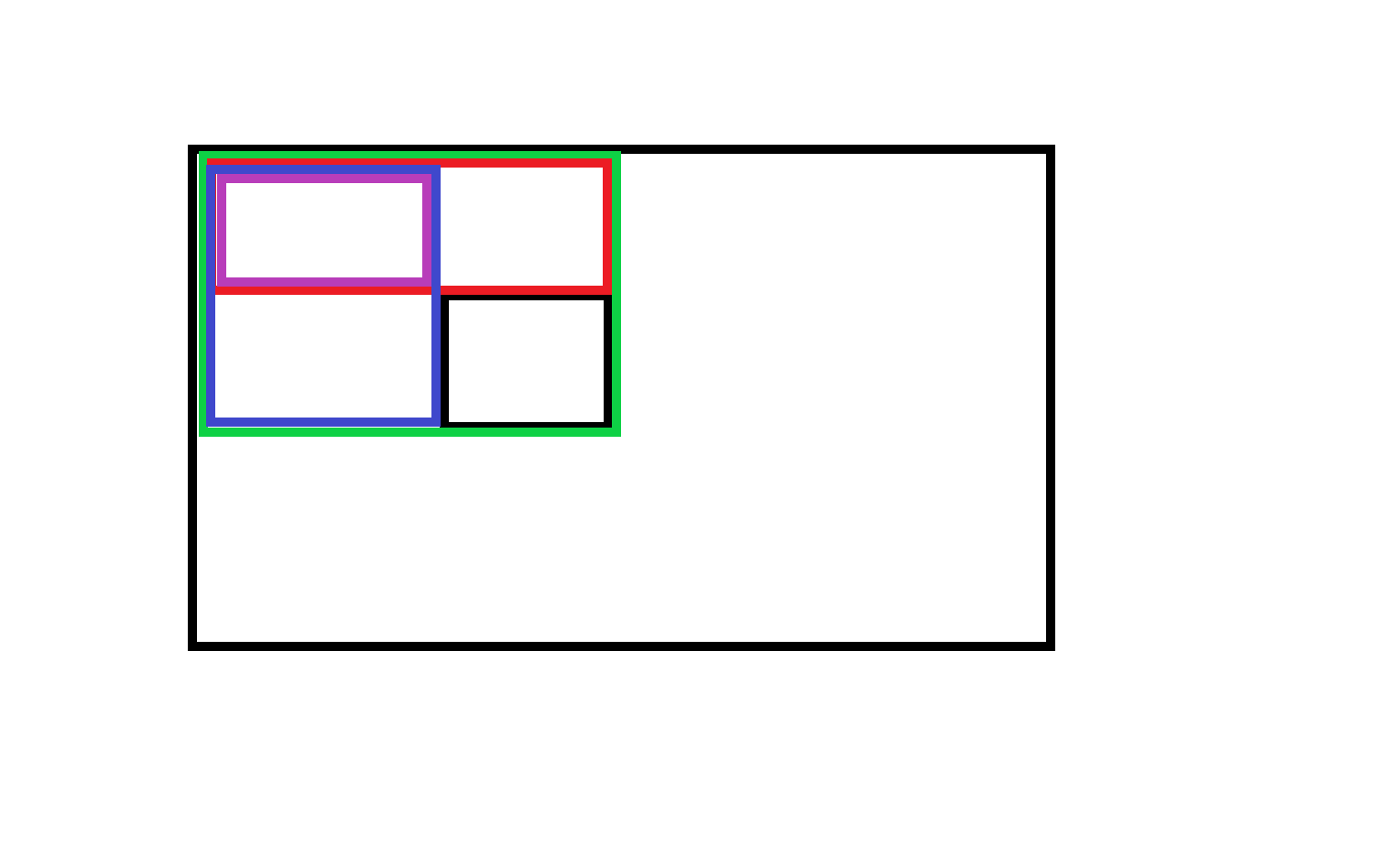
公式:S黑=S绿-S红-S蓝+S紫//这里我也不太好解释,具体看y总模板以及讲解
请看题目的模板:
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
cin >> a[i][j];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
while (q -- )
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
}
return 0;
}
快速写法
#include<iostream>
using namespace std;
const int N = 1010;
int n,m,q,a[N][N],s[N][N];
int main()
{
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
while(q--)
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<s[x2][y2]-s[x1 - 1][y2]-s[x2][y1-1]+s[x1-1][y1-1] << endl;
}
}
一维差分的原理
差分是前缀和的逆运算,
所以求差分数组更难并且要应用到前缀和的相关知识。
请看题目: ACWING.797差分
本题是一道差分题。
那有人要问了,凭啥用差分?
那我们就需要先了解差分的基本原理
我们构造一个数组b使a是b的前缀和,具体公式为:
s[i] += a[i],s[i + 1] -= a[i];
这一步表示将s[i]和s[i + 1]之间的所有元素加上a[i]
当然大家把s数组改成b数组也行(看个人习惯)
所以如果这个操作用朴素算法做的话那时间复杂度就会很高,而差分就能近乎 O1
妙哉!
模板献给大家:
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int s[N], a[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> s[i];
for (int i = 1; i <= n; i ++ ) a[i] = s[i] - s[i - 1];
while (m -- )
{
int l, r, c;
cin >> l >> r >> c;
a[l] += c, a[r + 1] -= c;
}
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
for (int i = 1; i <= n; i ++ ) cout << s[i] << ' ';
cout << endl;
return 0;
}
快速模板:
#include<iostream>
using namespace std;
const int N = 100010;
int n,m,a[N],s[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]+=a[i];
s[i+1]-=a[i];
}
while(m--)
{
int l,r,c;
cin>>l>>r>>c;
s[l]+=c;
s[r+1]-=c;
}
for(int i=1;i<=n;i++)
{
s[i]+=s[i-1];
cout<<s[i]<<' ';
}
}
二维差分——前方高能,请先学会前面的内容在来学习本BOSS
上来说三句:
此算法很难!!!
此算法很难!!!
此算法很难!!!
题目: ACWING.798差分矩阵
首先这里容斥原理的思路就不说了(刚在二维前缀和那里有图)
先说下让整个区域+c的公式操作:
void add(int x1,int y1,int x2,int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
容斥原理在此!
然后我们说下初始化:
差分矩阵的初始化就是把a设为b数组的前缀和。
调用函数add(刚写过的那个)
add(i,j,i,j,a[i][j]);
这样就初始化了一个点。
让a成为b的前缀和。
然后是模板:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &s[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
a[i][j] = s[i][j] - s[i - 1][j] - s[i][j - 1] + s[i - 1][j - 1];
while (q -- )
{
int x1, y1, x2, y2, c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
a[x1][y1] += c;
a[x1][y2 + 1] -= c;
a[x2 + 1][y1] -= c;
a[x2 + 1][y2 + 1] += c;
}
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ ) printf("%d ", s[i][j]);
cout << endl;
}
return 0;
}
快速模板:
#include<iostream>
using namespace std;
const int N = 1010;
int n,m,q,a[N][N],b[N][N];
void add(int x1,int y1,int x2,int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
cin >> n >> m >> q;
for(int i = 1; i<= n; i ++)
for(int j = 1; j <= m; j ++)
{
cin >> a[i][j];
add(i,j,i,j,a[i][j]);
}
while(q --)
{
int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
add(x1, y1, x2 ,y2,c);
}
for(int i = 1; i <= n; i ++, cout<<endl)
for(int j = 1; j <= m; j ++)
{
b[i][j] += b[i-1][j] + b[i][j - 1] -b[i - 1][j - 1];
cout<<b[i][j]<<' ';
}
}
抽风大佬提供超短板子:
#include <iostream>
using namespace std;
const int N=1005;
int a[N][N],b[N][N];
int main()
{
int n,m,k;
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
while(k--)
{
int x1,x2,y1,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
for(int i=1;i<=n;i++,puts(""))
for(int j=1;j<=m;j++)
b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1],printf("%d ",a[i][j]+b[i][j]);
return 0;
}
作者:垫底抽风
链接:https://www.acwing.com/blog/content/2575/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这期分享就先到这里了。
具体思路请报名算法基础课然后跟随y总思路学习(我这里只是大体讲一下)。
其他分享戳这里:
cht的分享

## 打卡
qaq
咳咳咳,一维前缀和saber版
可以
提两点讲解建议,一、s[r]代表什么,s[l-1]代表什么?要求的是什么。
二、有人认为二维较难的原因是因为画的都是点,如果画成格就非常容易理解,打到关键的四个点,在图中标出来
嗯,争取有时间改
加油!!!
谢谢~
二维差分简短模板~
知道的。谢谢~