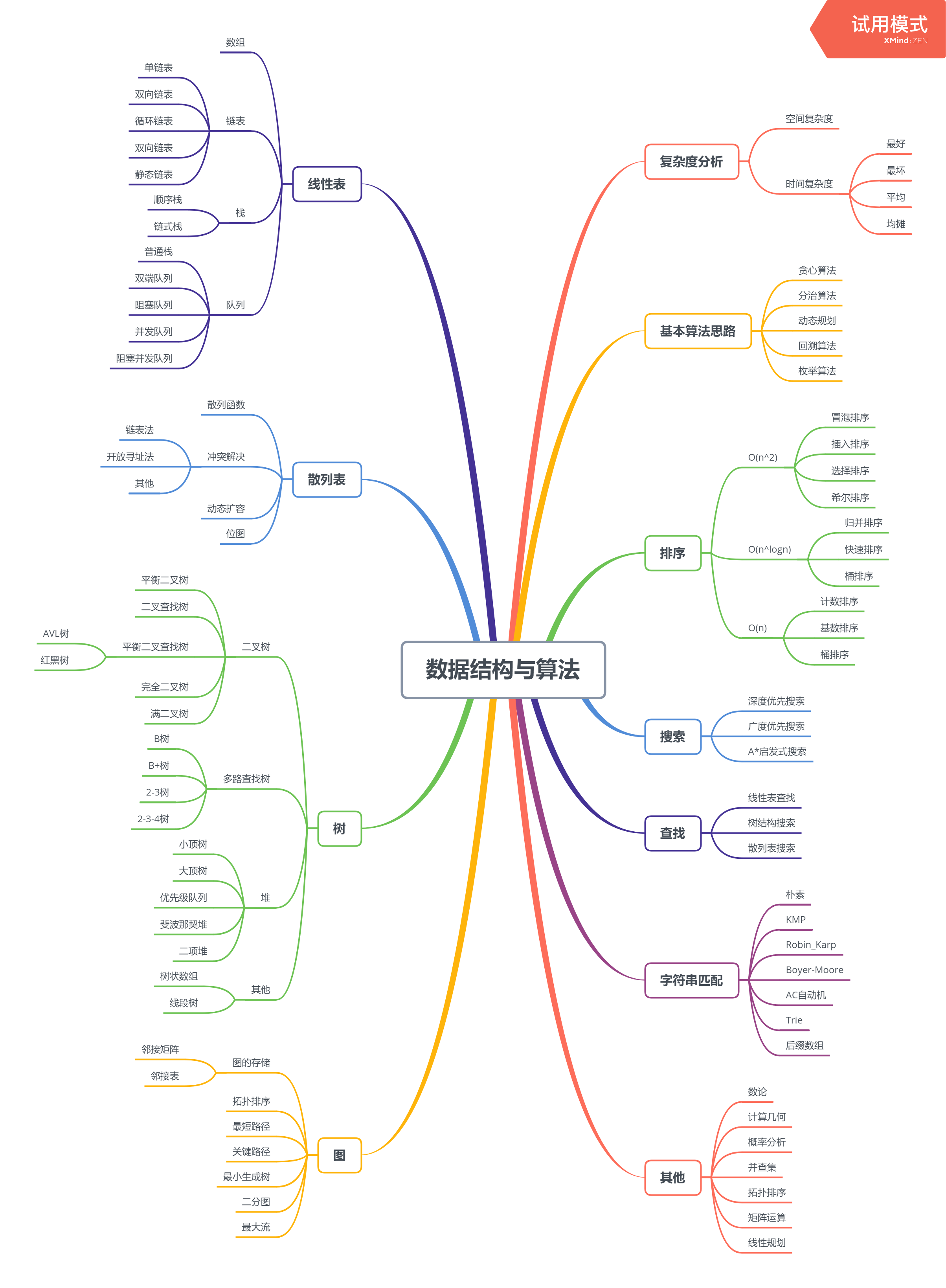
常用的数据结构与算法导图
相关的导图
数学组合部分总结
组合数2000内递推用空间换时间
#include <iostream>
using namespace std;
const int N = 2010, mod = 1e9+7;
int n;
int c[N][N];
void init() {
for(int i = 0; i < N; i++)
for(int j = 0; j <= i; j++)
if(!j) c[i][j] = 1;
else c[i][j] = (c[i-1][j-1] + c[i-1][j]) % mod;
}
int main() {
cin >> n;
init();
while(n--) {
int a, b;
cin >> a >> b;
cout << c[a][b] << endl;
}
return 0;
}
组合数 1e5内 预处理
快速幂的相关应用逆元
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5+10, mod = 1e9+7;
int n;
int fact[N], infact[N];
int qmi(int a, int k, int p) {
int ans = 1 % p;
while(k) {
if(k&1) ans = (LL)ans * a % p;
k >>= 1;
a = (LL) a * a % p;
}
return ans;
}
int main() {
cin >> n;
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i++) {
fact[i] = (LL)fact[i-1] * i % mod;
infact[i] = (LL)infact[i-1] * qmi(i, mod-2, mod) % mod;
}
while(n--) {
int a, b;
cin >> a >> b;
cout << ((LL)fact[a] * infact[a-b] % mod * infact[b]) % mod << endl;
}
return 0;
}
组合数 卢卡斯定理 a,b < 1e18.
不错的证明博客
#include <iostream>
using namespace std;
typedef long long LL;
int p;
// 特别要注意一些数据范围导致的溢出问题
LL qmi(LL a, int k, int p) {
LL ans = 1;
while(k) {
if(k&1) ans = ans * a % p;
k >>= 1;
a = a * a % p;
}
return ans;
}
LL C(LL a, LL b) {
LL ans = 1;
for(int i = 1, j = a; i <= b; i++, j--) {
ans = ans * j % p;
ans = ans * qmi(i, p-2, p) % p;
}
return ans;
}
LL lucas(LL a, LL b) {
if(a<p&&b<p) return C(a, b);
return ((LL)C(a%p, b%p)*lucas(a/p, b/p))%p;
}
int main() {
int n;
cin >> n;
while(n--) {
LL a, b;
cin >> a >> b >> p;
cout << lucas(a, b) << endl;
}
return 0;
}


大佬带带我呜呜呜
cao,NB
菜鸡不敢出声呜呜呜ORZ
您TQL,您ORZ,我%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%您
别搞hhh